题目内容
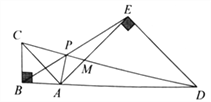
【题目】如图![]() ,已知
,已知![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 是
是![]() 边上的一个动点,连接
边上的一个动点,连接![]() ,
,![]() 的延长线交
的延长线交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .作
.作![]() 的外接圆
的外接圆![]() .设
.设![]() =
=![]() ,
,![]() =
=![]() .
.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若![]() 是
是![]() 的切线,求
的切线,求![]() 的值;
的值;
(3)过点________作________![]() ________,垂足为________,交
________,垂足为________,交![]() ________于点________,直线________交________于点________(如图
________于点________,直线________交________于点________(如图![]() ).若________=
).若________=![]() ,则
,则![]() ________的值是________.
________的值是________.
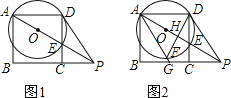
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)证明![]() ,利用相似比得到
,利用相似比得到![]() ,然后变形有
,然后变形有![]() ;
;
(2)连接![]() ,如图
,如图![]() ,根据圆周角定理得
,根据圆周角定理得![]() 是
是![]() 的直径,再利用切线的性质得
的直径,再利用切线的性质得![]() ,接着证明
,接着证明![]() ,利用相似比得到
,利用相似比得到![]() ,即
,即![]() =
=![]() ,与
,与![]() 联立可求出
联立可求出![]() 的值;
的值;
![]() 与
与![]() 的交点为
的交点为![]() ,连结
,连结![]() ,如图
,如图![]() ,在
,在![]() 中利用勾股定理计算出
中利用勾股定理计算出![]() =
=![]() ,再利用面积法计算出
,再利用面积法计算出![]() ,接着在
,接着在![]() 中利用勾股定理计算出
中利用勾股定理计算出![]() ,则可得到
,则可得到![]() ,根据圆周角定理得到
,根据圆周角定理得到![]() =
=![]() ,于是得到
,于是得到![]() .
.
解:(1)∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∴![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]()
∴![]() ;
;
(2)连接![]() ,如图
,如图![]() ,
,

∵![]() =
=![]() ,
,
∴![]() 是
是![]() 的直径,
的直径,
∵![]() 是
是![]() 的切线,
的切线,
∴![]() ,
,
∴![]() =
=![]() ,
,
∵![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵![]() =
=![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() =
=![]() ,
,
∵![]() ,
,
∴![]() =
=![]() ,
,
由于![]() ,则方程化为
,则方程化为![]() =
=![]() ,解得
,解得![]() =
=![]() ,
,![]() =
=![]() (舍去),
(舍去),
∴![]() 的值为
的值为![]() ;
;
(3)![]() 与
与![]() 的交点为
的交点为![]() ,连结
,连结![]() ,如图
,如图![]() ,
,
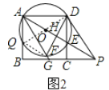
∵![]() =
=![]() ,
,
∴![]() 为
为![]() 的直径,
的直径,
在![]() 中,
中,
∵![]() =
=![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,∵
中,∵![]() ,
,![]() ,
,
∴![]() ,
,
∴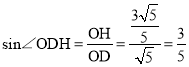 ,
,
∵![]() =
=![]() ,
,
∴![]() .
.
故答案为![]() .
.

练习册系列答案
相关题目