题目内容
【题目】如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA 上的动点,且AE=BF=CG=DH.

(1)求证:四边形EFGH是正方形;
(2)判断直线EG是否经过一个定点,并说明理由;
(3)求四边形EFGH面积的最小值。
【答案】(1)证明见解析;
(2)直线EG经过一个定点,这个定点为正方形的中心(AC、BD的交点);理由见解析;
(3)32cm2.
【解析】
试题分析:(1)由正方形的性质得出∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,证出AH=BE=CF=DG,由SAS证明△AEH≌△BFE≌△CGF≌△DHG,得出EH=FE=GF=GH,∠AEH=∠BFE,证出四边形EFGH是菱形,再证出∠HEF=90°,即可得出结论;
(2)连接AC、EG,交点为O;先证明△AOE≌△COG,得出OA=OC,证出O为对角线AC、BD的交点,即O为正方形的中心;
(3)设四边形EFGH面积为S,BE=xcm,则BF=(8-x)cm,由勾股定理得出S=x2+(8-x)2=2(x-4)2+32,S是x的二次函数,容易得出四边形EFGH面积的最小值.
试题解析:【解答】(1)证明:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵AE=BF=CG=DH,
∴AH=BE=CF=DG,
在△AEH、△BFE、△CGF和△DHG中,
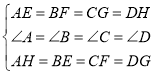
∴△AEH≌△BFE≌△CGF≌△DHG(SAS),
∴EH=FE=GF=GH,∠AEH=∠BFE,
∴四边形EFGH是菱形,
∵∠BEF+∠BFE=90°,
∴∠BEF+∠AEH=90°,
∴∠HEF=90°,
∴四边形EFGH是正方形;
(2)解:直线EG经过一个定点,这个定点为正方形的中心(AC、BD的交点);理由如下:
连接AC、EG,交点为O;如图所示:

∵四边形ABCD是正方形,
∴AB∥CD,
∴∠OAE=∠OCG,
在△AOE和△COG中,
 ,
,
∴△AOE≌△COG(AAS),
∴OA=OC,即O为AC的中点,
∵正方形的对角线互相平分,
∴O为对角线AC、BD的交点,即O为正方形的中心;
(3)解:设四边形EFGH面积为S,设BE=xcm,则BF=(8-x)cm,
根据勾股定理得:EF2=BE2+BF2=x2+(8-x)2,
∴S=x2+(8-x)2=2(x-4)2+32,
∵2>0,
∴S有最小值,
当x=4时,S的最小值=32,
∴四边形EFGH面积的最小值为32cm2.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案

