题目内容
 阅读理解题:下面利用45°角的正切,求tan22.5°的值,方法如下:
阅读理解题:下面利用45°角的正切,求tan22.5°的值,方法如下:
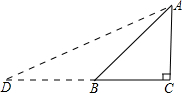
解:构造Rt△ABC,其中∠C=90°,∠B=45°,如图.
延长CB到D,使BD=AB,连接AD,则∠D= ∠ABC=22.5°.
∠ABC=22.5°.
设AC=a,则BC=a,AB=BD= a.
a.
又∵CD=BD+CB=(1+ )atan22.5°=tan∠D=
)atan22.5°=tan∠D=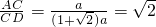 -1
-1
请你仿照此法求tan15°的值.
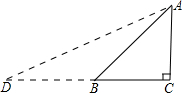
解:构造Rt△ABC,其中∠C=90°,∠ABC=30°,
延长CB到D,使BD=AB,连接AD,
则∠D= ∠ABC=15°,
∠ABC=15°,
设AC=a,则由构造的三角形得:
AB=2a,BC= a,BD=2a,
a,BD=2a,
则CD=2a+ a=(2+
a=(2+ )a,
)a,
∴tan15°=tanC= =
=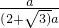 =2-
=2- .
.
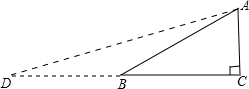
分析:同样按阅读构造Rt△ABC,其中∠C=90°,∠ABC=30°,延长CB到D,使BD=AB,连接AD,根据构造的直角三角形,设AC=a,再用a表示出CD,即可求出tan15°的值.
点评:此题考查的知识点是解直角三角形,关键是根据阅读构造含30°的直角三角形,再作辅助线得15°角的直角三角形,再设AC=a,表示出CD.
延长CB到D,使BD=AB,连接AD,
则∠D=
 ∠ABC=15°,
∠ABC=15°,设AC=a,则由构造的三角形得:
AB=2a,BC=
 a,BD=2a,
a,BD=2a,则CD=2a+
 a=(2+
a=(2+ )a,
)a,∴tan15°=tanC=
 =
=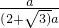 =2-
=2- .
.
分析:同样按阅读构造Rt△ABC,其中∠C=90°,∠ABC=30°,延长CB到D,使BD=AB,连接AD,根据构造的直角三角形,设AC=a,再用a表示出CD,即可求出tan15°的值.
点评:此题考查的知识点是解直角三角形,关键是根据阅读构造含30°的直角三角形,再作辅助线得15°角的直角三角形,再设AC=a,表示出CD.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 阅读理解题:下面利用45°角的正切,求tan22.5°的值,方法如下:
阅读理解题:下面利用45°角的正切,求tan22.5°的值,方法如下:
 •
•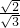 =
=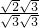 =
= .
.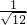 =______=______;②
=______=______;②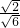 =______=______;
=______=______; ﹢
﹢ -3)(______)使其结果不再含有根号;同样请你仿照(1)的方法将下列二次根式化简:
-3)(______)使其结果不再含有根号;同样请你仿照(1)的方法将下列二次根式化简: .
.