题目内容
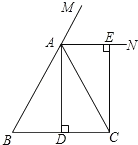
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
【答案】(1)证明见解析(2)当△ABC满足∠BAC=90°时,四边形ADCE是一个正方形.
【解析】试题分析:(1)根据矩形的有三个角是直角的四边形是矩形,已知CE⊥AN,AD⊥BC,所以求证∠DAE=90°,可以证明四边形ADCE为矩形.
(2)根据正方形的判定,我们可以假设当AD=![]() BC,由已知可得,DC=
BC,由已知可得,DC=![]() BC,由(1)的结论可知四边形ADCE为矩形,所以证得,四边形ADCE为正方形.
BC,由(1)的结论可知四边形ADCE为矩形,所以证得,四边形ADCE为正方形.
试题解析:(1)证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,
∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE,
∴∠DAE=∠DAC+∠CAE=![]() ×180°=90°,
×180°=90°,
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形.
(2)当△ABC满足∠BAC=90°时,四边形ADCE是一个正方形.
理由:∵AB=AC,
∴∠ACB=∠B=45°,
∵AD⊥BC,
∴∠CAD=∠ACD=45°,
∴DC=AD,
∵四边形ADCE为矩形,
∴矩形ADCE是正方形.
∴当∠BAC=90°时,四边形ADCE是一个正方形.

练习册系列答案
相关题目