题目内容
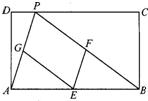 25、如图,矩形ABCD中,AB=a,AD=b,P是边DC上的任意一点,连接PA、PB,点E、F、G分别是AB、BP、PA的中点.
25、如图,矩形ABCD中,AB=a,AD=b,P是边DC上的任意一点,连接PA、PB,点E、F、G分别是AB、BP、PA的中点.(1)求证:四边形EFPG是平行四边形;
(2)试猜想:当P位于什么位置时,四边形EFPG是菱形?并证明猜想的正确性;
(3)以下是小慧和小聪的一段对话:

你赞成谁的观点?如果赞成小慧,请说明理由;如果赞成小聪,请直接写出a与b之间的关系式.
分析:(1)运用两组对边分别平行的四边形是平行四边形进行证明;
(2)当P位于DC中点时,四边形EFPG是菱形.先由矩形的性质,得∠D=∠C=90°,DA=CB,再根据中点的定义证明△DAP≌△CBP,从而得PA=PB,再根据中点的定义证得PG=PF,根据一组邻边相等的平行四边形得证四边形EFPG是菱形.
(3)小慧的观点正确,由一组邻边相等的平行四边形可得菱形,只要P为DC的中点,△DAP≌△CBP时,PA=PB,平行四边形EFDG即为菱形,所以与a、b之间的关系无关.
(2)当P位于DC中点时,四边形EFPG是菱形.先由矩形的性质,得∠D=∠C=90°,DA=CB,再根据中点的定义证明△DAP≌△CBP,从而得PA=PB,再根据中点的定义证得PG=PF,根据一组邻边相等的平行四边形得证四边形EFPG是菱形.
(3)小慧的观点正确,由一组邻边相等的平行四边形可得菱形,只要P为DC的中点,△DAP≌△CBP时,PA=PB,平行四边形EFDG即为菱形,所以与a、b之间的关系无关.
解答:(1)证明:∵点E、F、G分别是AB、BP、PA的中点,
∴EG∥PB,EF∥PA,∴四边形EFPG是平行四边形.
(2)解:当P位于DC中点时,四边形EFPG是菱形.
证明:∵四边形ABCD是矩形,∴∠D=∠C=90°,DA=CB.
又∵P为DC中点,∴DP=CP.
∴△DAP≌△CBP,∴PA=PB.
∵F、G分别是PB、PA的中点,
∴PG=PF.
又∵四边形EFPG是平行四边形,
∴四边形EFPG是菱形.
(3)解:我赞成小慧的观点,理由如下:
由(2)知,只要PA=PB,四边形EFDG即为菱形.
即当P为DC的中点,△DAP≌△CBP时,PA=PB.这与a、b之间的关系无关.
∴EG∥PB,EF∥PA,∴四边形EFPG是平行四边形.
(2)解:当P位于DC中点时,四边形EFPG是菱形.
证明:∵四边形ABCD是矩形,∴∠D=∠C=90°,DA=CB.
又∵P为DC中点,∴DP=CP.
∴△DAP≌△CBP,∴PA=PB.
∵F、G分别是PB、PA的中点,
∴PG=PF.
又∵四边形EFPG是平行四边形,
∴四边形EFPG是菱形.
(3)解:我赞成小慧的观点,理由如下:
由(2)知,只要PA=PB,四边形EFDG即为菱形.
即当P为DC的中点,△DAP≌△CBP时,PA=PB.这与a、b之间的关系无关.
点评:解答此类题的关键是要突破思维定势的障碍,运用发散思维,多方思考,探究问题在不同条件下的不同结论,挖掘它的内在联系,向“纵、横、深、广”拓展,从而寻找出添加的条件和所得的结论.

练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
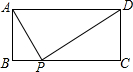 如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )
如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )A、a≥
| ||
| B、a≥b | ||
C、a≥
| ||
| D、a≥2b |
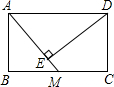 如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为
如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为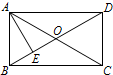 7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE=
7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE= (2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为
(2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为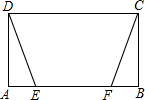 (2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.
(2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.