题目内容
13、已知等腰Rt△ABC（如图），试取斜边AB上的一点为圆心画图，使点A，B，C分别在所画的圆内、圆外和圆上．分析：利用等腰三角形的性质，以及点与圆的位置关系判定方法，可以依次确定A，B，C与圆的位置关系．
解答：解：作中线CD，在线段OA上取一点O，以O为圆心，OA为半径画圆即可．
理由：∵△ABC为等腰直角三角形，
∴DA=DB=DC，
Rt△COD中，OC为斜边，则OC＞CD，OA＜AD=CD，故A在圆内，
OB＞BD=CD，故B在圆外，
显然C在圆上．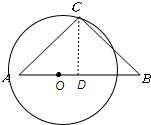
理由：∵△ABC为等腰直角三角形，
∴DA=DB=DC，
Rt△COD中，OC为斜边，则OC＞CD，OA＜AD=CD，故A在圆内，
OB＞BD=CD，故B在圆外，
显然C在圆上．
点评：此题主要考查了等腰三角形的性质，点与圆的位置关系的判定．
练习册系列答案
全能测控期末小状元系列答案
相关题目
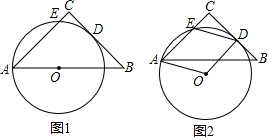
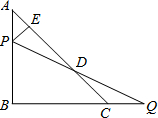（2012•深圳二模）如图，已知等腰Rt△ABC中，∠B=90°，AB=BC=8cm，点P是线段AB上的点，点Q是线段BC延长线上的点，且AP=CQ，PQ与直线AC相交于点D．作PE⊥AC于点E，则线段DE的长度（ ）
（2012•拱墅区二模）如图，已知等腰Rt△ABC中，∠ACB=90°，点D为等腰Rt△ABC内一点，∠CAD=∠CBD=15°，E为AD延长线上的一点，且CE=CA．
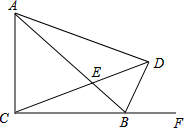如图，已知等腰Rt△ABC中，∠ACB=90°，AC=BC=4，D为△ABC的一个外角∠ABF的平分线上一点，且∠ADC=45°，CD交AB于E，