题目内容
【题目】如图，在平面直角坐标系xOy中，直线l：y=kx+m交y轴于点C，与抛物线y=ax2+bx交于点A（4，0）、B（-
，-
）．
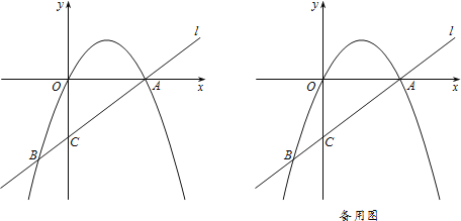
（1）直线l的表达式为：______，抛物线的表达式为：______；
（2）若点P是二次函数y=ax2+bx在第四象限内的图象上的一点，且2S△APB=S△AOB，求△AOP的面积；
（3）若点Q是二次函数图象上一点，设点Q到直线l的距离为d，到抛物线的对称轴的距离为d1，当|d-d1|=2时，请直接写出点Q的坐标．
【答案】（1）y=
x-3，y=-
x2+2x；（2）S△AOP=
；（3）点Q的坐标为（
，2-3）或（-，-3-2）或（6，-6）或（-1，-
）或（1，
）或（-4，-16）或（4，0）．
【解析】
（1）将点A、B坐标代入一次函数、抛物线表达式即可求解；
（2）将直线l沿y轴向下平移
个单位长度得直线y=
x
，交二次函数在第四象限内的图象于点P，即可求解；
（3）确定d=QRcosα=|
x2+2x
x+3|×
，d1=|x-2|，利用|d-d1|=2，即可求解．
解：（1）将点A、B坐标代入一次函数表达式：y=kx+m得：
，
解得：
，
∴直线的表达式为：y=x-3，
同理将点A、B的坐标代入抛物线表达式，得
，
解得：a=，b=2，
∴抛物线的表达式为：y=x2+2x；
（2）将直线l向下平移m个单位，交抛物线于点P，交y轴于点D，
过点P、D分别作直线l的垂线HD、PM于点H、M，过点O作直线PD的垂线交直线l于点F、交直线PD于点E，
则PM=HD，2S△APB=S△AOB，则PM=HD=2OF，
直线的表达式为：y=x-3，则tan∠HCD=tan∠OCF，
即：
，
解得：OC=
OC=，
∵FC∥ED
∴
，
∴
，
即：x-
=-x2+2x，
解得：x=或-2（舍去负值），
点P（，-
），
S△AOP=
=
；
（3）过点Q分别作直线l和函数对称轴的垂线交于点H、G，过点Q作QR∥y轴交直线l和x轴于点R、S，
则∠RQH=∠RAS=α，直线AB表达式得k值为，即tanα=，则cosα=，
设点Q（x，-x2+2x）、则点R（x，x-3），
d=QRcosα=|-x2+2x-x+3|×…①，
d1=|x-2|…②，
|d-d1|=2…③，
联立①②③并解得：x=
或-或6或-1或1或4或-4，
故点Q的坐标为：（，2-3）或（-，-3-2）或（6，-6）或（-1，-
）或（1，）或（-4，-16）或（4，0）．
