题目内容
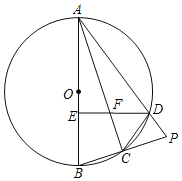
【题目】如图，扇形ABC的圆心角为90°，半径为6，将扇形ABC绕A点逆时针旋转得到扇形ADE，点B、C的对应点分别为点D、E，若点D刚好落在
上，则阴影部分的面积为_____．
【答案】3π+9
．
【解析】
直接利用旋转的性质结合扇形面积求法以及等边三角形的判定与性质得出S阴影＝S扇形ADE﹣S弓形AD＝S扇形ABC﹣S弓形AD，进而得出答案.
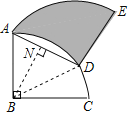
解：连接BD，过点B作BN⊥AD于点N，
∵将半径为4，圆心角为90°的扇形BAC绕A点逆时针旋转60°，
∴∠BAD＝60°，AB＝AD，
∴△ABD是等边三角形，
∴∠ABD＝60°，
则∠ABN＝30°，
故AN＝3，BN＝3，
S阴影＝S扇形ADE﹣S弓形AD＝S扇形ABC﹣S弓形AD
＝
﹣（
﹣
×6×3）
＝3π+9．
故答案为3π+9．
练习册系列答案
相关题目
【题目】某品牌电脑销售公司有营销员14人，销售部为制定营销人员月销售电脑定额，统计了这14人某月的销售量如下（单位：台）：
销售量 | 200 | 170 | 130 | 80 | 50 | 40 |
人数 | 1 | 1 | 2 | 5 | 3 | 2 |
（1）该公司营销员销售该品牌电脑的月销售平均数是 台，中位数是 台，众数是 台．
（2）销售部经理把每位营销员月销售量定为90台，你认为是否合理？说明理由．
