题目内容
 20、如图所示,已知直线AM、DF,C、E分别在直线AM、DF上,小华想知道∠ACE和∠DEC是否互补,但是他没有带量角器,只带了一副三角板,于是他想了这样一个办法:首先连接CF,再指出CF的中点O,然后连接EO并延长EO和直线AM相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.以下是他的想法,请你填上根据.
20、如图所示,已知直线AM、DF,C、E分别在直线AM、DF上,小华想知道∠ACE和∠DEC是否互补,但是他没有带量角器,只带了一副三角板,于是他想了这样一个办法:首先连接CF,再指出CF的中点O,然后连接EO并延长EO和直线AM相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.以下是他的想法,请你填上根据.小华是这样想的:
因为CF和BE相交于点O,
根据
对顶角相等
得出∠COB=∠EOF;而O是CF的中点,那么CO=FO,又已知EO=BO,
根据
SAS
得出△COB≌△FOE,根据
全等三角形的对应边相等
得出BC=EF,根据
全等三角形的对应角相等
得出∠BCO=∠F.既然∠BCO=∠F,根据
内错角相等
得出AB∥DF,既然AB∥DF,根据
两直线平行,同旁内角互补
得出∠ACE和∠DEC互补分析:本题通过全等三角形得到内错角相等,得到两直线平行,进而得到同旁内角互补.
解答:解:因为CF和BE相交于点O,
根据对顶角相等得出∠COB=∠EOF;
而O是CF的中点,那么CO=FO,又已知EO=BO,
根据SAS得出△COB≌△FOE,
根据全等三角形的对应边相等得出BC=EF,
根据全等三角形的对应角相等得出∠BCO=∠F.
既然∠BCO=∠F,根据内错角相等得出AB∥DF,
既然AB∥DF,根据两直线平行,同旁内角互补得出∠ACE和∠DEC互补.
故结果分别为:对顶角相等;SAS;全等三角形的对应边相等;全等三角形的对应角相等;内错角相等;两直线平行,同旁内角互补.
根据对顶角相等得出∠COB=∠EOF;
而O是CF的中点,那么CO=FO,又已知EO=BO,
根据SAS得出△COB≌△FOE,
根据全等三角形的对应边相等得出BC=EF,
根据全等三角形的对应角相等得出∠BCO=∠F.
既然∠BCO=∠F,根据内错角相等得出AB∥DF,
既然AB∥DF,根据两直线平行,同旁内角互补得出∠ACE和∠DEC互补.
故结果分别为:对顶角相等;SAS;全等三角形的对应边相等;全等三角形的对应角相等;内错角相等;两直线平行,同旁内角互补.
点评:本题重在考查三角形的全等的判定和性质;做题时用了两直线平行内错角相等,同旁内角互补等知识,要学会综合运用这些知识.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由. 4、如图所示,已知直线a∥b,被直线L所截,如果∠1=69°36′,那么∠2=
4、如图所示,已知直线a∥b,被直线L所截,如果∠1=69°36′,那么∠2= 平移,设平移过程中△F′O′G′与四边形ODCE重叠部分面积为y,OO′的长为x(0≤x≤1),求y与x的函数关系式.
平移,设平移过程中△F′O′G′与四边形ODCE重叠部分面积为y,OO′的长为x(0≤x≤1),求y与x的函数关系式.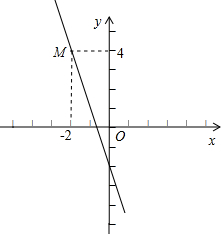 如图所示,已知直线y=kx-2经过M点,求此直线与x轴交点坐标和直线与两坐标轴围成三角形的面积.
如图所示,已知直线y=kx-2经过M点,求此直线与x轴交点坐标和直线与两坐标轴围成三角形的面积. 如图所示:已知直线y=
如图所示:已知直线y=