题目内容
 阅读下列材料:
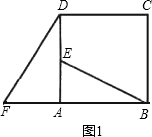
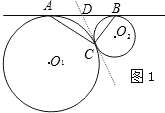
阅读下列材料:如图1,⊙O1和⊙O2外切于点C,AB是⊙O1和⊙O2外公切线,A、B为切点,
求证:AC⊥BC
证明:过点C作⊙O1和⊙O2的内公切线交AB于D,
∵DA、DC是⊙O1的切线
∴DA=DC.
∴∠DAC=∠DCA.
同理∠DCB=∠DBC.
又∵∠DAC+∠DCA+∠DCB+∠DBC=180°,
∴∠DCA+∠DCB=90°.
即AC⊥BC.
根据上述材料,解答下列问题:
(1)在以上的证明过程中使用了哪些定理?请写出两个定理的名称或内容;
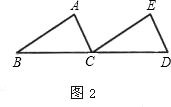
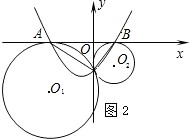
(2)以AB所在直线为x轴,过点C且垂直于AB的直线为y轴建立直角坐标系(如图2),已知A、B两点的坐标为(-4,0),(1,0),求经过A、B、C三点的抛物线y=ax2+bx+c的函数解析式;
(3)根据(2)中所确定的抛物线,试判断这条抛物线的顶点是否落在两圆的连心O1O2上,并说明理由.
分析:(1)由切线长相等可知用了切线长定理;由三角形的内角和是180°,可知用了三角形内角和定理;
(2)先根据勾股定理求出C点坐标,再用待定系数法即可求出经过A、B、C三点的抛物线的函数解析式;
(3)过C作两圆的公切线,交AB于点D,由切线长定理可求出D点坐标,根据C,D两点的坐标可求出过C,D两点直线的解析式,根据过一点且互相垂直的两条直线解析式的关系可求出过两圆圆心的直线解析式,再把抛物线的顶点坐标代入直线的解析式看是否适合即可.
(2)先根据勾股定理求出C点坐标,再用待定系数法即可求出经过A、B、C三点的抛物线的函数解析式;
(3)过C作两圆的公切线,交AB于点D,由切线长定理可求出D点坐标,根据C,D两点的坐标可求出过C,D两点直线的解析式,根据过一点且互相垂直的两条直线解析式的关系可求出过两圆圆心的直线解析式,再把抛物线的顶点坐标代入直线的解析式看是否适合即可.
解答:解:(1)DA、DC是⊙O1的切线,
∴DA=DC.应用的是切线长定理;
∠DAC+∠DCA+∠DCB+∠DBC=180°,应用的是三角形内角和定理.
(2)设C点坐标为(0,y),则AB2=AC2+BC2,
即(|-4-1|)2=(-4)2+y2+12+y2,
即25=17+2y2,解得y=2(舍去)或y=-2.
故C点坐标为(0,-2),
设经过A、B、C三点的抛物线的函数解析式为y=ax2+bx+c,
则
,
解得
,
故所求二次函数的解析式为y=
x2+
x-2.
(3)过C作两圆的公切线CD交AB于D,则AD=BD=CD,由A(-4,0),B(1,0)可知D(-
,0),
设过CD两点的直线为y=kx+b,则
,
解得
,
故此一次函数的解析式为y=-
x-2,
∵过O1,O2的直线必过C点且与直线y=-
x-2垂直,
故过O1,O2的直线的解析式为y=-
x-2.
由(2)中所求抛物线的解析式可知抛物线的顶点坐标为(
,-
),
代入直线解析式得-
×
-2=-
,故这条抛物线的顶点落在两圆的连心O1O2上.
∴DA=DC.应用的是切线长定理;
∠DAC+∠DCA+∠DCB+∠DBC=180°,应用的是三角形内角和定理.
(2)设C点坐标为(0,y),则AB2=AC2+BC2,
即(|-4-1|)2=(-4)2+y2+12+y2,
即25=17+2y2,解得y=2(舍去)或y=-2.
故C点坐标为(0,-2),
设经过A、B、C三点的抛物线的函数解析式为y=ax2+bx+c,
则
|

解得
|
故所求二次函数的解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
(3)过C作两圆的公切线CD交AB于D,则AD=BD=CD,由A(-4,0),B(1,0)可知D(-
| 3 |
| 2 |
设过CD两点的直线为y=kx+b,则
|
解得
|
故此一次函数的解析式为y=-
| 4 |
| 3 |
∵过O1,O2的直线必过C点且与直线y=-
| 4 |
| 3 |
故过O1,O2的直线的解析式为y=-
| 3 |
| 4 |
由(2)中所求抛物线的解析式可知抛物线的顶点坐标为(
| 3 |
| 2 |
| 25 |
| 8 |
代入直线解析式得-
| 3 |
| 4 |
| 3 |
| 2 |
| 25 |
| 8 |
点评:此题是一道材料分析题.解答时要阅读材料,获得解题思路,并根据两圆外切的条件作出辅助线,结合抛物线和直线的性质解答.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目