题目内容
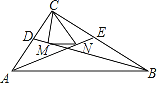
【题目】如图,四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4).点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直x轴于点P,连接AC交NP于Q,连接MQ.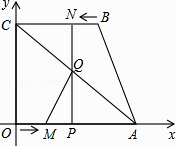
(1)点(填M或N)能到达终点;
(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;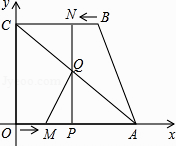
(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.
【答案】
(1)M
(2)
解:经过t秒时,NB=t,OM=2t,
则CN=3﹣t,AM=4﹣2t,
∵A(4,0),C(0,4),
∴AO=CO=4,
∵∠AOC=90°,
∴∠BCA=∠MAQ=45°,
∴QN=CN=3﹣t
∴PQ=1+t,
∴S△AMQ= ![]() AMPQ=
AMPQ= ![]() (4﹣2t)(1+t)=﹣t2+t+2.
(4﹣2t)(1+t)=﹣t2+t+2.
∴S=﹣t2+t+2=﹣t2+t﹣ ![]() +
+ ![]() +2=﹣(t﹣
+2=﹣(t﹣ ![]() )2+
)2+ ![]() ,
,
∵0≤t≤2
∴当 ![]() 时,S的值最大.
时,S的值最大.
(3)
解:存在.
设经过t秒时,NB=t,OM=2t
则CN=3﹣t,AM=4﹣2t
∴∠BCA=∠MAQ=45°
①若∠AQM=90°,则PQ是等腰Rt△MQA底边MA上的高
∴PQ是底边MA的中线
∴PQ=AP= ![]() MA
MA
∴1+t= ![]() (4﹣2t)
(4﹣2t)
∴t= ![]()
∴点M的坐标为(1,0)
②若∠QMA=90°,此时QM与QP重合
∴QM=QP=MA
∴1+t=4﹣2t
∴t=1
∴点M的坐标为(2,0)
【解析】(1)(BC÷点N的运动速度)与(OA÷点M的运动速度)可知点M能到达终点.(2)经过t秒时可得NB=y,OM﹣2t.根据∠BCA=∠MAQ=45°推出QN=CN,PQ的值.求出S与t的函数关系式后根据t的值求出S的最大值.(3)本题分两种情况讨论(若∠AQM=90°,PQ是等腰Rt△MQA底边MA上的高;若∠QMA=90°,QM与QP重合)求出t值.

【题目】6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频数分布直方图如下:

(1)直接写出a的值,并补全频数分布直方图.
分组 | 频数 | 频率 |
49.5~59.5 | 0.08 | |
59.5~69.5 | 0.12 | |
69.5~79.5 | 20 | |
79.5~89.5 | 32 | |
89.5~100.5 | a |
(2)若成绩在80分以上(含80分)为优秀,求这次参赛的学生中成绩为优秀的约为多少人?
(3)若这组被抽查的学生成绩的中位数是80分,请直接写出被抽查的学生中得分为80分的至少有多少人?