Question

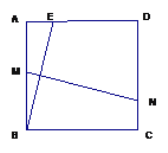
【题目】如图，四边形ABCD内接于⊙O，AB是直径，C为的中点，延长AD，BC交于点P，连结AC．

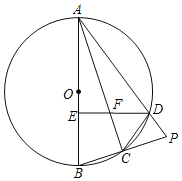
（1）求证：AB＝AP；

（2）若AB＝10，DP＝2，

①求线段CP的长；

②过点D作DE⊥AB于点E，交AC于点F，求△ADF的面积．

Answer 1

【答案】（1）见解析；（2）①PC＝；②S△ADF＝．

【解析】

（1）利用等角对等边证明即可；

（2）①利用勾股定理分别求出BD，PB，再利用等腰三角形的性质即可解决问题；

②作FH⊥AD于H，首先利用相似三角形的性质求出AE，DE，再证明AE=AH，设FH=EF=x,利用勾股定理构建方程解决问题即可.

（1）证明：∵＝，

∴∠BAC＝∠CAP，

∵AB是直径，

∴∠ACB＝∠ACP＝90°，

∵∠ABC+∠BAC＝90°，∠P+∠CAP＝90°，

∴∠ABC＝∠P，

∴AB＝AP．

（2）

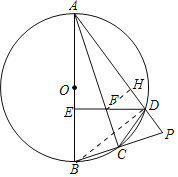
①解：连接BD．

∵AB是直径，

∴∠ADB＝∠BDP＝90°，

∵AB＝AP＝10，DP＝2，

∴AD＝10﹣2＝8，

∴BD＝＝＝6，

∴PB＝＝＝2，

∵AB＝AP，AC⊥BP，

∴BC＝PC＝PB＝，

∴PC＝．

②解：作FH⊥AD于H．

∵DE⊥AB，

∴∠AED＝∠ADB＝90°，

∵∠DAE＝∠BAD，

∴△ADE∽△ABD，

∴＝＝，

∴＝＝，

∴AE＝，DE＝，

∵∠FEA＝∠FEH，FE⊥AE，FH⊥AH，

∴FH＝FE，∠AEF＝∠AHF＝90°，

∵AF＝AF，

∴Rt△AFE≌Rt△AFH（HL），

∴AH＝AE＝，DH＝AD﹣AH＝，设FH＝EF＝x，

在Rt△FHD中，则有（﹣x）2＝x2+（）2，

解得x＝，

∴S△ADF＝ADFH＝×8×＝．

故答案为①PC＝；②S△ADF＝．