题目内容
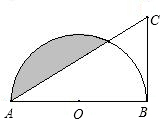 如图,AB是半圆O的直径,∠BAC=30°,BC为半圆的切线,切点为B,且BC=4\sqrt{3}.
如图,AB是半圆O的直径,∠BAC=30°,BC为半圆的切线,切点为B,且BC=4\sqrt{3}.(1)求圆心O到AC的距离;
(2)求阴影部分的面积.
分析:(1)首先在Rt△ABC中,根据∠BAC的度数以及BC的长,可求出⊙O的直径;过O作AC的垂线,设垂足为E,在Rt△OAE中,根据⊙O的半径及∠BAC的度数,即可求得OE.
(2)连接OD,阴影部分的面积即为扇形OAD和△OAD的面积差;扇形圆心角∠AOD的度数易求得,而AD的长,可由AB•sinA得出,由此得解.
(2)连接OD,阴影部分的面积即为扇形OAD和△OAD的面积差;扇形圆心角∠AOD的度数易求得,而AD的长,可由AB•sinA得出,由此得解.
解答: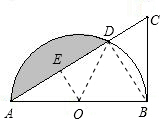 解:(1)过O作OE⊥AC于E;
解:(1)过O作OE⊥AC于E;
∵BC是圆的切线,
∴∠ABC=90°
∵∠BAC=30°,BC=4
.
∴AB=
=12,
∴AO=6;
∵∠ABC=∠OEA,
又∠ABC=∠EAO,
∴sin∠ABC=sin∠EAO=30°,
∴OE=
AO=3.
(2)连接OD、BD;
∵∠AOD=2∠AOE=120°,
在Rt△ABD中,AD=AB•cosA=6
;
∴S扇形=
=12π,S△AOD=
AD•OE=
×6
×3=9
;
∴S阴影=S扇形-S△AOD=12π-9
.
 解:(1)过O作OE⊥AC于E;
解:(1)过O作OE⊥AC于E;∵BC是圆的切线,
∴∠ABC=90°
∵∠BAC=30°,BC=4
| 3 |
∴AB=
| BC |
| tan30° |
∴AO=6;
∵∠ABC=∠OEA,
又∠ABC=∠EAO,
∴sin∠ABC=sin∠EAO=30°,
∴OE=
| 1 |
| 2 |
(2)连接OD、BD;
∵∠AOD=2∠AOE=120°,
在Rt△ABD中,AD=AB•cosA=6
| 3 |
∴S扇形=
| 120•π•62 |
| 360 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴S阴影=S扇形-S△AOD=12π-9
| 3 |
点评:此题主要考查的是切线的性质、图形面积的求法以及解直角三角形的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,AB是半圆O的直径,AC是弦,点P从点B开始沿BA边向点A以1cm/s的速度移动,若AB长为10cm,点O到AC的距离为4cm.
如图,AB是半圆O的直径,AC是弦,点P从点B开始沿BA边向点A以1cm/s的速度移动,若AB长为10cm,点O到AC的距离为4cm. 已知:如图,AB是半圆O的直径,OD是半径,BM切半圆于点B,OC与弦AD平行交BM于点C.
已知:如图,AB是半圆O的直径,OD是半径,BM切半圆于点B,OC与弦AD平行交BM于点C. 如图,AB是半圆O的直径,点D是半圆上一动点,AB=10,AC=8,当△ACD是等腰三角形时,点D到AB的距离是
如图,AB是半圆O的直径,点D是半圆上一动点,AB=10,AC=8,当△ACD是等腰三角形时,点D到AB的距离是 如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列结论:①S△O′OE=
如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列结论:①S△O′OE=
