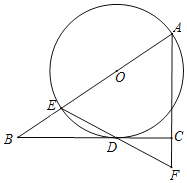题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD为斜边AB的中线.过点D作AB的垂线交AC于点E,再过A、D、E三点作⊙O.
(1)确定⊙O的圆心O的位置,并证明CD为⊙O的切线;
(2)若BC=3,求⊙O的直径.
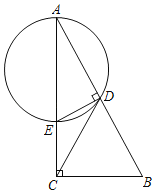
【答案】(1)圆心O在AE的中点处,见解析;(2)2![]()
【解析】
(1)求出∠ADE=90°,根据圆周角定理求出AE为直径,即可得出答案;求出OD⊥DC,根据切线的判定得出即可;
(2)解直角三角形求出AB,求出AD,解直角三角形求出AE即可.
(1)解:∵点D在⊙O上,DE⊥AB,
∴∠ADE=90°,
∴AE为⊙O的直径,
∴圆心O在AE的中点处;
证明:连接OD,
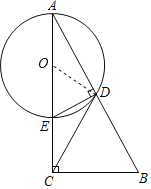
∵∠A=30°,
∴∠COD=2∠A=60°,
∵在Rt△ACB中,CD为斜边AB上的中线,
∴CD=![]() AB=AD,
AB=AD,
∴∠OCD=∠A=30°,
∴∠ODC=180°﹣60°﹣30°=90°,
即OD⊥DC,
∵OD过O,
∴CD为⊙O的切线;
(2)解:∵在Rt△ABC中,∠A=30°,BC=3,
∴AB=2BC=6,
∵D为AB的中点,
∴AD=BD=3,
在Rt△ADE中,AE=![]() =
=![]() =2
=2![]() ,
,
∴⊙O的直径为2![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】2019年2月18日,《感动中国2018年度人物颁奖盛典》在央视综合频道播出,其中乡村教师张玉滚的事迹令人非常感动某校团委组织“支援乡村教育,帮助教师张玉滚”的捐款活动,以下为九年级(1)班捐款情况:
捐款金额(元) | 5 | 10 | 20 | 50 |
人数(人) | 12 | 13 | 16 | 11 |
则这个班学生捐款金额的中位数和众数分别为( )
A.15,50B.20,20C.10,20D.20,50
【题目】二次函数y=ax![]() +bx+c的x,y的对应值如下表:
+bx+c的x,y的对应值如下表:
x | … | -1 |
| 0 |
| 1 |
| 2 | … |
y | … | -1 |
| m |
| 1 |
| n | … |
下列关于该函数性质的判断:①该二次函数有最大值;②当x>0时,函数y随x的增大而减小;③不等式y<﹣1的解集是﹣1<x<2;④关于x的一元二次方程ax2+bx+c=0的两个实数根分别位于﹣1<x<![]() 和
和![]() <x<2之间.其中正确结论的个数有( )
<x<2之间.其中正确结论的个数有( )
A.1个B.2个C.3个D.4个