题目内容
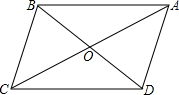
如图，已知平行四边形ABCD中，∠ABC、∠BCD的平分线BE、CF分别交边AD于E、F．求证：AF=ED．
证明：∵四边形ABCD是平行四边形，
∴AB=CD，AD∥BC，
∴∠AEB=∠EBC，
∵BE平分∠ABC，
∴∠ABE=∠CBE，
∴∠ABE=∠AEB，
∴AB=AE，
同理DF=CD，
∴AE=DF，
即AE-EF=DF-EF，
∴AF=DE．
∴AB=CD，AD∥BC，
∴∠AEB=∠EBC，
∵BE平分∠ABC，
∴∠ABE=∠CBE，
∴∠ABE=∠AEB，
∴AB=AE，
同理DF=CD，
∴AE=DF，
即AE-EF=DF-EF，
∴AF=DE．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
