题目内容
如图所示,矩形AOBC在直角坐标系中,O为原点,A在x轴上,B在y轴上,直线AB的函数关系式为y=-| 4 | 3 |
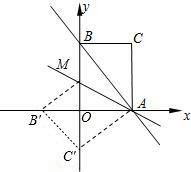 点B′处,C的对应点为C′.
点B′处,C的对应点为C′.(1)求出B′点和M点的坐标;
(2)求直线A C′的函数关系式;
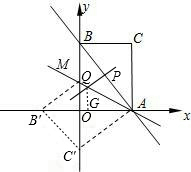
(3)设一动点P从A点出发,以每秒1个单位速度沿射线AB方向运动,过P作PQ⊥AB,交射线AM于Q;
①求运动t秒时,Q点的坐标;(用含t的代数式表示)
②以Q为圆心,以PQ的长为半径作圆,当t为何值时,⊙Q与y轴相切?
分析:结合图形,考虑到折叠后的图形与原图形的全等关系即可求得.
解答:解:(1)由一次函数y=-
x+8可知A(6,0),B(0,8),
由Rt△AOB可得OA=6,OB=8,AB=10,AB′=10,
B′的坐标为(-4,0),
设BM=a,则B′M=a,OM=8-a,在Rt△MOB′中OM2+OB′2=BM2,
即(8-a)2+42=a2,解得a=5,
故OM=3,
M点的坐标为:(0,3);
(2)△ABC沿AM翻转后变成△AB′C′,故△ABC≌△AB′C′,tan∠CAB=tan∠C′BA′=
,
∴AC′的斜率为
,
∵A点坐标为(6,0)
∴AC′的解析式为y=
(x-6);
(3)由题意,点P坐标为(6-
t,-
),作QG⊥x轴,
∴AG=AP=t,
∴①Q(6-t,)或(6-t,
)
∴②当t=4或12秒.
| 4 |
| 3 |
由Rt△AOB可得OA=6,OB=8,AB=10,AB′=10,
B′的坐标为(-4,0),
设BM=a,则B′M=a,OM=8-a,在Rt△MOB′中OM2+OB′2=BM2,
即(8-a)2+42=a2,解得a=5,
故OM=3,
M点的坐标为:(0,3);
(2)△ABC沿AM翻转后变成△AB′C′,故△ABC≌△AB′C′,tan∠CAB=tan∠C′BA′=
| 3 |
| 4 |
∴AC′的斜率为
| 3 |
| 4 |

∵A点坐标为(6,0)
∴AC′的解析式为y=
| 3 |
| 4 |
(3)由题意,点P坐标为(6-
| 3 |
| 5 |
| 4 |
| 5 |
∴AG=AP=t,
∴①Q(6-t,)或(6-t,
| t-6 |
| 2 |
∴②当t=4或12秒.
点评:本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变.

练习册系列答案
相关题目
 15、如图所示,矩形ABCD的对角线相交于O,AE平分∠BAD,交BC于E,∠CAE=15°,那么∠AOB=
15、如图所示,矩形ABCD的对角线相交于O,AE平分∠BAD,交BC于E,∠CAE=15°,那么∠AOB=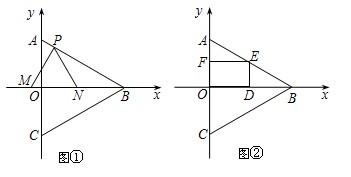
 边在△AOB内部作如图所示的矩形ODEF,点E在线段AB上.
边在△AOB内部作如图所示的矩形ODEF,点E在线段AB上. 如图所示,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的对角线AC的长是
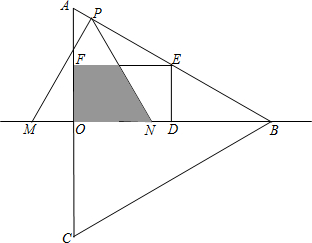
如图所示,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的对角线AC的长是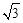 个单位的速度运动,设运动时间为t秒.以点P为顶点,作等边△PMN,点M,N在x轴上.
个单位的速度运动,设运动时间为t秒.以点P为顶点,作等边△PMN,点M,N在x轴上.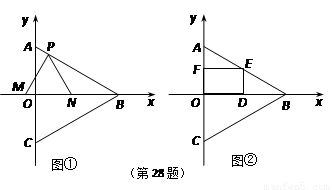
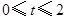 秒时S与
秒时S与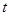 的函数关系式,并求出S的最大值.
的函数关系式,并求出S的最大值.