题目内容
如图①,在平面直角坐标系中,已知△ABC是等边三角形,点B的坐标为(12,0),动点P在线段AB上从点A向点B以每秒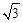 个单位的速度运动,设运动时间为t秒.以点P为顶点,作等边△PMN,点M,N在x轴上.
个单位的速度运动,设运动时间为t秒.以点P为顶点,作等边△PMN,点M,N在x轴上.
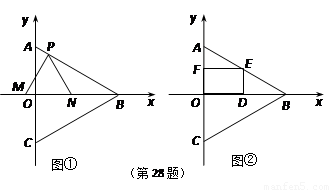
1.当t为何值时,点M与点O重合.
2.求点P坐标和等边△PMN的边长(用t的代数式表示).
3.如果取OB的中点D,以OD为边在△AOB内部作如图②所示的矩形ODEF,点E在线段AB上.设等边△PMN和矩形ODEF重叠部分的面积为S,请求出当 秒时S与
秒时S与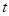 的函数关系式,并求出S的最大值.
的函数关系式,并求出S的最大值.
1.(1)如图①,点M与点O重合.
∵△ABC是等边三角形,∴∠ABO=30°,∠BAO=60°.由OB=12,∴AB=8 ,AO=4
,AO=4 .
.
∵△PON是等边三角形,∴∠PON=60°.∴∠AOP=60°.∴AO=2AP,即4 =2
=2 t.解得t=2.∴当t=2时,点M与点O重合.
t.解得t=2.∴当t=2时,点M与点O重合.
2.(2)如图②,过P分别作PQ⊥OA于点Q,PS⊥OB于点S.
可求得AQ= AP=
AP=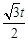 ,PS=QO=4
,PS=QO=4 -
-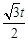 .
.
∴点P坐标为( ,4
,4 -
-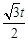 ). ………………6分
). ………………6分
在Rt△PMS中,sin60°=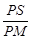 ,
,
∴PM=(4 -
-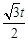 )÷
)÷ =8-t.
=8-t.

3.(3)(Ⅰ)当0≤t≤1时,见图③.
设PN交EF于点G,则重叠部分为直角梯形FONG,作GH⊥OB于点H.
∵∠GNH=60°,GH=2 ,∴HN=2.∵MP=8-t,∴BM=2MP=16-2t.
,∴HN=2.∵MP=8-t,∴BM=2MP=16-2t.
∴OM=BM-OB=16-2t-12=4-2t.∴ON=MN-OM=8-t-(4-2t)=4+t.
∴FG=OH=ON-HN=4+t-2=2+t. ∴S= (2+t+4+t)×2
(2+t+4+t)×2 =2
=2 t+6
t+6 .
.
∵S随t的增大而增大,∴当t=1时,S最大=8 .…10分
.…10分

(Ⅱ)当1<t≤2时,见图④.设PM交EF于点I,交FO于点Q,PN交EF于点G.
重叠部分为五边形OQIGN.
OQ=4 -2
-2 t,FQ=2
t,FQ=2 -(4
-(4 -2
-2 t)= 2
t)= 2 t-2
t-2 ,
,
FI= FQ=2t-2.
FQ=2t-2.
∴三角形QFP的面积= (2
(2 t-2
t-2 )(2t-2)=
2
)(2t-2)=
2 (t2-2t+1).
(t2-2t+1).
由(Ⅰ)可知梯形OFGN的面积=2 t+6
t+6 ,
,
∴S=2 t+6
t+6 -2
-2 (t2-2t+1)=-2
(t2-2t+1)=-2 (t2-3t-2).
(t2-3t-2).
∵-2 <0,∴当t=
<0,∴当t= 时,S有最大值,S最大=
时,S有最大值,S最大= .
.
综上所述:当0≤t≤1时,S=2 t+6
t+6 ;当1<t≤2时,S=-2
;当1<t≤2时,S=-2 t2+6
t2+6 t+4
t+4 ;
;
∵ >8
>8 ,∴S的最大值是
,∴S的最大值是 .
.

【解析】略

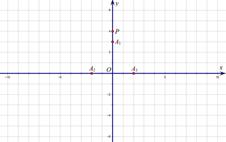
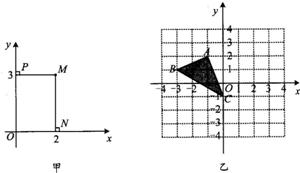 23、在数学上,为了确定平面上点的位置,我们常用下面的方法:如图甲,在平面内画两条互相垂直,并且有公共原点O的数轴,通常一条画成水平,叫x轴,另一条画成铅垂,叫y轴,这样,我们就说在平面上建立了一个平面直角坐标系,这是由法国数学家和哲学家笛卡尔创立的,这样我们就能确定平面上点的位置,例如,要确定点M的位置,只要作MP⊥x轴,MP⊥y轴,设垂足N,P在各自数轴上所表示的数分别为x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),(1)△ABC在平面直角坐标系中的位置如图乙,请把△ABC向右平移3个单位,在平面直角坐标系中画出平移后的△A′B′C′;
23、在数学上,为了确定平面上点的位置,我们常用下面的方法:如图甲,在平面内画两条互相垂直,并且有公共原点O的数轴,通常一条画成水平,叫x轴,另一条画成铅垂,叫y轴,这样,我们就说在平面上建立了一个平面直角坐标系,这是由法国数学家和哲学家笛卡尔创立的,这样我们就能确定平面上点的位置,例如,要确定点M的位置,只要作MP⊥x轴,MP⊥y轴,设垂足N,P在各自数轴上所表示的数分别为x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),(1)△ABC在平面直角坐标系中的位置如图乙,请把△ABC向右平移3个单位,在平面直角坐标系中画出平移后的△A′B′C′;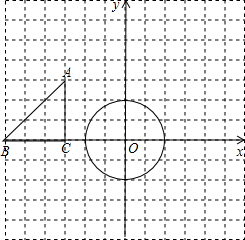 在平面直角坐标系中,将一块腰长为
在平面直角坐标系中,将一块腰长为
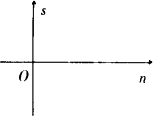
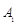 为旋转中心时,点
为旋转中心时,点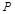 绕着点
绕着点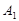 旋转180°得到
旋转180°得到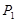 点,点
点,点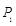 再绕着点
再绕着点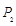 点,这时点
点,这时点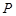 与点
与点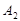 为旋转中心时,点
为旋转中心时,点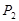 点,点
点,点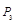 点,点
点,点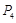 点,小明发现P、
点,小明发现P、 两点关于点
两点关于点 中心对称.
中心对称.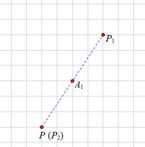
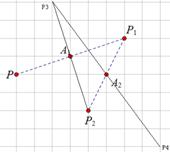
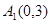 、
、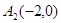 、
、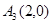 为旋转中心时,点
为旋转中心时,点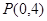 绕着点
绕着点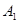 旋转180°得到
旋转180°得到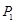 点;点
点;点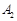 旋转180°得到
旋转180°得到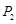 点;点
点;点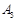 旋转180°得到
旋转180°得到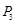 点;点
点;点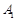 旋转180°得到点
旋转180°得到点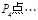 . 继续如此操作若干次得到点
. 继续如此操作若干次得到点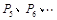 ,则点
,则点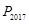 的坐为.
的坐为.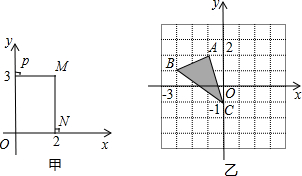 ,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),
,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),