Question

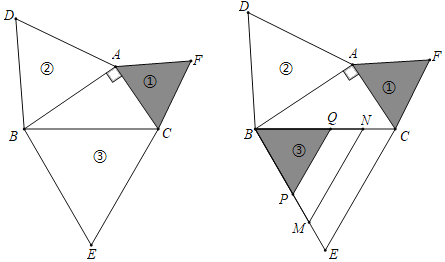
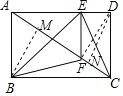
【题目】如图，矩形ABCD中，E为边AD上一点（不为端点），EF⊥AD交AC于点F，要求△FBC的面积，只需知道下列哪个三角形的面积即可（　　）

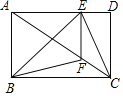
A.△EBCB.△EBFC.△ECDD.△EFC

Answer 1

【答案】C

【解析】

连接DF、过B作BM⊥AC于点M，过D作DN⊥AC于N，证明△ADN≌△CBM得DN＝BM，由三角形的面积公式可得△BCF和△CDE的面积都等于△CDF的面积，便可得出答案．

解：连接DF、过B作BM⊥AC于点M，过D作DN⊥AC于N，

∵四边形ABCD是矩形，

∴AD＝BC，AD∥BC，

∴∠DAC＝∠ACB，

在△ADN和△CBM中，

，

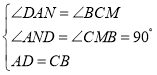∴△ADN≌△CBM（AAS），

∴DN＝BM，

∵，，

∴S△BCF＝S△CDF，

∵EF⊥AD，∠ADC＝90°，

∴EF∥CD，

∴，，

∴S△CDE＝S△CDF＝S△BCF，

故选：C．