题目内容
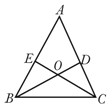
【题目】如图,△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于点O,则图中有_______对全等三角形.
【答案】3.
【解析】首先证明△ACE≌△ABD可得AD=AE,EC=BD,根据等式的性质可得AB-AE=AC-AD,即EB=DC;再证明△EBC≌△DCB,△EOB≌△DOC即可.
解:△ACE≌△ABD,△EBC≌△DCB,△EOB≌△DOC,
∵BD、CE为高,
∴∠ADB=∠AEC=,90°,
在△AEC和△ADB中,
∠A=∠A,∠AEC=∠ADB,AB=AC,
∴△ACE≌△ABD(ASA);
∴AD=AE,EC=BD,
∴AB-AE=AC-AD,
即EB=DC,
在△EBC和△DCB中,
EB=DC,BC=BC,EC=DB,∴△EBC≌△DCB(SSS),
在△EOB和△DOC中,
EB=DC,∠OEB=∠ODC,∠EOB=∠DOC,
∴△EOB≌△DOC(AAS).
故答案为:3.
“点睛”本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】(2016山东省聊城市第21题)为了让书籍开拓学生的视野,陶冶学生的情操,向阳中学开展了“五个一”课外阅读活动,为了解全校学生课外阅读情况,抽样调查了50名学生平均每天课外阅读时间(单位:min),将抽查得到的数据分成5组,下面是尚未完成的频数、频率分布表:
组别 | 分组 | 频数(人数) | 频率 |
1 | 10≤t<30 | 0.16 | |
2 | 30≤t<50 | 20 | |
3 | 50≤t<70 | 0.28 | |
4 | 70≤t<90 | 6 | |
5 | 90≤t<110 |
(1)将表中空格处的数据补全,完成上面的频数、频率分布表;
(2)请在给出的平面直角坐标系中画出相应的频数直方图;
(3)如果该校有1500名学生,请你估计该校共有多少名学生平均每天阅读时间不少于50min?
