Question

【题目】如图，以扇形OAB的顶点O为原点，半径OB所在的直线为x轴建立平面直角坐标系，点B的坐标为（2，0），扇形的圆心角是60°，若抛物线 y=x+k与扇形OAB的边界总有两个公共点，则实数取值范围是

A. -4＜k＜ B. -2＜k＜

C. -4＜k＜ D. --2＜k＜

Answer 1

【答案】A

【解析】由图可知，∠AOB=60°，

∴直线OA的解析式为y=x，联立，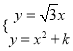

消掉y得，x-x+k=0,△=（-）-4×1×k=0，即k=时，

抛物线与OA有一个交点，解得：x=，即交点的横坐标为，

∵点B的坐标为（2，0），∴OA=2，∴点A的坐标为（1， ）

∵<1,∴交点在线段AO上；

当抛物线经过点B（2，0）时，4+k=0，解得k=-4，

∴要使抛物线y=x+k与扇形OAB的边界总有两个公共点，实数k的取值范围是：-4＜k＜．故选A．