题目内容
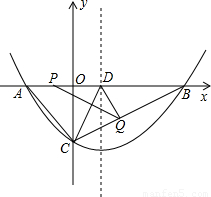
已知抛物线y=ax2+bx+c(a>0)的图象经过点B(14,0)和C(0,-8),对称轴为x=4.(1)求该抛物线的解析式;
(2)点D在线段AB上且AD=AC,若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动,同时另一动点Q以某一速度从C出发沿线段CB匀速运动,问是否存在某一时刻,使线段PQ被直线CD垂直平分?若存在,请求出此时的时间(秒)和点Q的运动速度;若不存在,请说明理由.
【答案】分析:(1)把点B、C的坐标代入抛物线解析式,根据对称轴解析式列出关于a、b、c的方程组,求解即可;
(2)根据抛物线解析式求出点A的坐标,再利用勾股定理列式求出AC的长,然后求出OD,可得点D在抛物线对称轴上,根据线段垂直平分线上的性质可得∠PDC=∠QDC,PD=DQ,再根据等边对等角可得∠PDC=∠ACD,从而得到∠QDC=∠ACD,再根据内错角相等,两直线平行可得PQ∥AC,再根据点D在对称轴上判断出DQ是△ABC的中位线,根据三角形的中位线平行于第三边并且等于第三边的一半求出DQ= AC,再求出AP,然后根据时间=路程÷速度求出点P运动的时间t,根据勾股定理求出BC,然后求出CQ,根据速度=路程÷时间,计算即可求出点Q的速度.
AC,再求出AP,然后根据时间=路程÷速度求出点P运动的时间t,根据勾股定理求出BC,然后求出CQ,根据速度=路程÷时间,计算即可求出点Q的速度.
解答:解:(1)∵图象经过点B(14,0)和C(0,-8),对称轴为x=4,
∴ ,
,
解得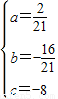 ,
,
∴抛物线的解析式为y=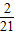 x2-
x2-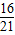 x-8;
x-8;
(2)存在直线CD垂直平分PQ.
理由如下:令y=0,则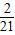 x2-
x2-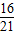 x-8=0,
x-8=0,
整理得,x2-8x-84=0,
解得x1=-6,x2=14(为点B坐标),
∴点A的坐标为(-6,0),
在Rt△AOC中,AC=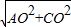 =
=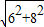 =10,
=10,
∴OD=AD-AO=AC-AO=10-6=4,
∴点D在二次函数的对称轴上,
∵直线CD垂直平分PQ,
∴∠PDC=∠QDC,PD=DQ,
又∵AD=AC,
∴∠PDC=∠ACD,
∴∠QDC=∠ACD,
∴DQ∥AC,
∴DQ是△ABC的中位线,
∴DQ= AC=
AC= ×10=5,
×10=5,
∴AP=AD-PD=AC-DQ=10-5=5,
∵动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动,
∴t=5÷1=5,
∴存在t=5(秒)时,线段PQ被直线CD垂直平分,
此时,在Rt△BOC中,BC=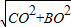 =
=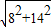 =2
=2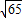 ,
,
∵DQ是△ABC的中位线,
∴CQ= BC=
BC= ×2
×2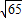 =
=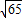 ,
,
∴点Q的运动速度为每秒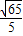 单位长度.
单位长度.
点评:本题是二次函数综合题型,主要考查了待定系数法求二次函数解析式,线段垂直平分线上的点到线段两端点的距离相等的性质,勾股定理,等边对等角的性质,三角形的中位线平行于第三边并且等于第三边的一半,(2)求出DQ∥AC是解题的关键.
(2)根据抛物线解析式求出点A的坐标,再利用勾股定理列式求出AC的长,然后求出OD,可得点D在抛物线对称轴上,根据线段垂直平分线上的性质可得∠PDC=∠QDC,PD=DQ,再根据等边对等角可得∠PDC=∠ACD,从而得到∠QDC=∠ACD,再根据内错角相等,两直线平行可得PQ∥AC,再根据点D在对称轴上判断出DQ是△ABC的中位线,根据三角形的中位线平行于第三边并且等于第三边的一半求出DQ=
 AC,再求出AP,然后根据时间=路程÷速度求出点P运动的时间t,根据勾股定理求出BC,然后求出CQ,根据速度=路程÷时间,计算即可求出点Q的速度.
AC,再求出AP,然后根据时间=路程÷速度求出点P运动的时间t,根据勾股定理求出BC,然后求出CQ,根据速度=路程÷时间,计算即可求出点Q的速度.解答:解:(1)∵图象经过点B(14,0)和C(0,-8),对称轴为x=4,
∴
 ,
,解得
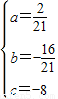 ,
,∴抛物线的解析式为y=
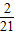 x2-
x2-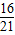 x-8;
x-8;(2)存在直线CD垂直平分PQ.
理由如下:令y=0,则
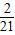 x2-
x2-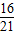 x-8=0,
x-8=0,整理得,x2-8x-84=0,
解得x1=-6,x2=14(为点B坐标),
∴点A的坐标为(-6,0),
在Rt△AOC中,AC=
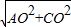 =
=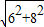 =10,
=10,∴OD=AD-AO=AC-AO=10-6=4,
∴点D在二次函数的对称轴上,
∵直线CD垂直平分PQ,
∴∠PDC=∠QDC,PD=DQ,
又∵AD=AC,
∴∠PDC=∠ACD,
∴∠QDC=∠ACD,
∴DQ∥AC,
∴DQ是△ABC的中位线,
∴DQ=
 AC=
AC= ×10=5,
×10=5,∴AP=AD-PD=AC-DQ=10-5=5,
∵动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动,
∴t=5÷1=5,
∴存在t=5(秒)时,线段PQ被直线CD垂直平分,
此时,在Rt△BOC中,BC=
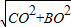 =
=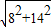 =2
=2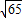 ,
,∵DQ是△ABC的中位线,
∴CQ=
 BC=
BC= ×2
×2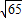 =
=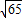 ,
,∴点Q的运动速度为每秒
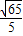 单位长度.
单位长度.点评:本题是二次函数综合题型,主要考查了待定系数法求二次函数解析式,线段垂直平分线上的点到线段两端点的距离相等的性质,勾股定理,等边对等角的性质,三角形的中位线平行于第三边并且等于第三边的一半,(2)求出DQ∥AC是解题的关键.

练习册系列答案
相关题目
 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=