题目内容
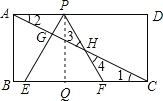
【题目】如图,已知矩形ABCD,AB=![]() ,BC=3,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
,BC=3,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
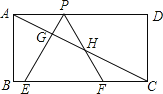
(1)求△PEF的边长;
(2)在不添加辅助线的情况下,当F与C不重合时,从图中找出一对相似三角形,并说明理由;
(3)求证:PH﹣BE=1.
【答案】(1)2;(2)△APH∽△CFH;(3)见解析
【解析】解:(1)过P作PQ⊥BC于Q.
∵矩形ABCD中,∠B=90°,即AB⊥BC,
又∵AD∥BC,
∴PQ=AB=![]() ,
,
∵△PEF是等边三角形,
∴∠PFQ=60°.
在Rt△PQF中,PF=![]() =
=![]() =2,
=2,
∴△PEF的边长为2;
(2)△APH∽△CFH.
理由:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠1=∠2,
∵∠3=∠4,
∴△APH∽△CFH;
(3)在Rt△ABC中,AB=![]() ,BC=3,
,BC=3,
∴AC=![]() =2
=2![]() ,
,
∴∠ACB=30°,
∵△PEF是等边三角形,
∴∠2=60°,PF=EF=2,
∵∠2=∠1+∠3,
∴∠3=30°,
∴∠1=∠3,
∴FC=FH,
∵PH+FH=2,BE+FC=3﹣EF=3﹣2=1,
∴PH﹣BE=1.

练习册系列答案
相关题目