题目内容
【题目】如图，直线l1，l2交于点B，A是直线l1上的点，在直线l2上寻找一点C，使△ABC是等腰三角形，请画出所有的等腰三角形．
【答案】4个
【解析】试题分析:本题考查等腰三角形的构造方法,题目中已经给出线段AB,在直线l2上寻找一点C,使△ABC是等腰三角形,则需要进行分类讨论,以线段AB为腰和线段AB为底边两种情况进行画图,画图方法简称:”两圆一线”法.
试题解析:具体作法如下,如图，
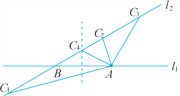
（1）当以线段AB为腰时,点A为顶点时,可以以点A为圆心,线段AB为半径画圆,圆与直线l2 的交点即为点C,此时有1个,
（2）当以线段AB为腰时,点B为顶点时,可以以点B为圆心,线段BA为半径画圆,圆与直线l2 的交点即为点C,此时有2个,
（3）当以线段AB为底边,可以作线段AB的垂直平分线,线段垂直平分线与直线l2 的交点即为点C,此时有1个.
故共有4个满足题意的等腰三角形.
点睛:本题主要考查等腰三角形的构造问题,解决本题的关键在于理解掌握”两圆一线”法求满足条件的点.
暑假作业安徽少年儿童出版社系列答案【题目】某人去水果批发市场采购苹果，他看中了A、B两家苹果．这两家苹果品质一样，零售价都为6元/千克，批发价各不相同．A家规定：批发数量不超过1000千克，按零售价的92%优惠；批发数量不超过2000千克，按零售价的90%优惠；超过2000千克的按零售价的88%优惠．B家的规定如下表：
数量范围（千克） | 0～500 | 500以上～1500 | 1500以上～2500 | 2500以上 |
价 格（元） | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
[表格说明：批发价格分段计算，如：某人批发苹果2100千克，则总费用=6×95%×500+6×85%×1000+6×75%×（2100﹣1500）]
（1）如果他批发600千克苹果，则他在A 家批发需要元，在B家批发需要元；
（2）如果他批发x千克苹果（1500＜x＜2000），则他在A 家批发需要元，在B家批发需要元（用含x的代数式表示）；
（3）现在他要批发1800千克苹果，你能帮助他选择在哪家批发更优惠吗？请说明理由．
