题目内容
将点A（4，0）绕着原点顺时针方向旋转30°得到点B，则点B的坐标是
（2
，-2）
| 3 |
（2
，-2）
．| 3 |
分析：作出草图，根据旋转的性质求出OB，过点B作BC⊥x轴于C，根据直角三角形30°角所对的直角边等于斜边的一半求出BC，再利用勾股定理列式求出OC，然后写出点B的坐标即可．
解答：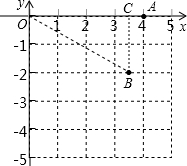
解：如图，∵点A（4，0），
∴OA=3，
连接OB，过点B作BC⊥x轴于C，
则OB=OA，
∵旋转角为30°，
∴∠BOC=30°，
∴BC=
OB=
×4=2，
在Rt△OBC中，OC=
=
=2
，
∴点B的坐标为（2
，-2）．
故答案为：（2
，-2）．
解：如图，∵点A（4，0），∴OA=3，
连接OB，过点B作BC⊥x轴于C，
则OB=OA，
∵旋转角为30°，
∴∠BOC=30°，
∴BC=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OBC中，OC=
| OB2-BC2 |
| 42-22 |
| 3 |
∴点B的坐标为（2
| 3 |
故答案为：（2
| 3 |
点评：本题考查了坐标与图形变化-旋转，主要利用了旋转变换只改变图形的位置不改变图形的形状与大小的性质，直角三角形30°角所对的直角边等于斜边的一半的性质，熟记性质是解题的关键，作出图形更形象直观．
练习册系列答案
相关题目
将点A（2
，0）绕着原点顺时针方向旋转60°得到点B，则点B的坐标是（ ）
| 3 |
A、（
| ||
B、（
| ||
C、（3，-
| ||
D、（3，
|