题目内容
将点A(4
,0)绕着原点按顺时针旋转45°得到点B,则B点坐标是( )
| 2 |
分析:作出图形,过点B作BC⊥x轴于C,判断出△OBC是等腰直角三角形,根据等腰直角三角形的性质求出OC=BC=4,再写出点B的坐标即可.
解答: 解:如图,过点B作BC⊥x轴于C,
解:如图,过点B作BC⊥x轴于C,
∵点A(4
,0),
∴OB=OA=4
,
∵旋转角是45°,
∴△OBC是等腰直角三角形,
∴OC=BC=4
×
=4,
∴点B的坐标为(4,-4).
故选B.
 解:如图,过点B作BC⊥x轴于C,
解:如图,过点B作BC⊥x轴于C,∵点A(4
| 2 |
∴OB=OA=4
| 2 |
∵旋转角是45°,
∴△OBC是等腰直角三角形,
∴OC=BC=4
| 2 |
| ||
| 2 |
∴点B的坐标为(4,-4).
故选B.
点评:本题考查了坐标与图形性质-旋转,主要利用了等腰直角三角形的判定与性质,作出图形更形象直观.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
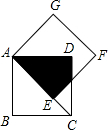 如图,将边长为2的正方形ABCD绕顶点A旋转,使点B落在AC上的点E处,得正方形AEFG,则两正方形重合部分(阴影部分)的面积是
如图,将边长为2的正方形ABCD绕顶点A旋转,使点B落在AC上的点E处,得正方形AEFG,则两正方形重合部分(阴影部分)的面积是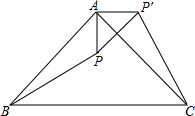 如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP绕点A逆时针旋转后与△ACP′重含.若P点到P′的距离为
如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP绕点A逆时针旋转后与△ACP′重含.若P点到P′的距离为