题目内容
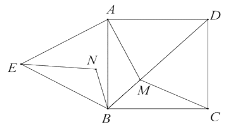
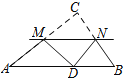
【题目】如图，在△ABC中，∠C＝90°，将△ABC沿直线MN翻折后，顶点C恰好落在边AB上的点D处，已知MN∥AB，MC＝6，NC＝2
，则四边形MABN的面积是___________.
【答案】18
【解析】
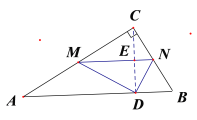
如图，连接CD，与MN交于点E，根据折叠的性质可知CD⊥MN，CE=DE.再根据相似三角形的判定可知△MNC∽△ABC,再根据相似三角形的面积之比等于相似比的平方.由图可知四边形ABNM的面积等于△ABC的面积减去△MNC的面积.
解:连接CD，交MN于点E.
∵△ABC沿直线MN翻折后，顶点C恰好落在边AB上的点D处，
∴CD⊥MN，CE=DE.
∵MN∥AB，
∴△MNC∽△ABC, CD⊥AB，
∴
=
=
=4.
∵
=
MC
CN=
6
2
=6,
∴
=24,
∴四边形ACNM=-
=24-6
=18
故答案是18.
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
【题目】国际上通常用恩格尔系数（记作n）来衡量一个国家和地区人民的生活水平的状况，它的计算公式：n=x/y（x：家庭食品支出总额；y：家庭消费支出总额）．各种家庭类型的n如下表：
已知王先生居住地2008年比2003年食品价格上升了25%，该家庭在2008年购买食品和2003年完全相同的情况下多支出2000元，并且y=2x+3600（单位：元），则该家庭2003年属于（ ）
家庭类型 | 贫困 | 温饱 | 小康 | 富裕 |
n | n＞60% | 50%＜n≤60% | 40%＜n≤50% | 30%＜n≤40% |
A. 贫困 B. 温饱 C. 小康 D. 富裕
