题目内容
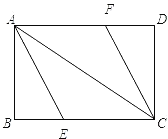
【题目】矩形ABCD中![]() 平分
平分![]() 交BC于
交BC于![]() 平分
平分![]() 交AD于F.
交AD于F.
(1)说明四边形AECF为平行四边形;
(2)求四边形AECF的面积.
【答案】(1)见解析;(2)30cm2
【解析】试题分析:
(1)由四边形ABCD是矩形可得AD∥BC(即AF∥CE),AB∥CD,由此可得∠BAC=∠ACD,结合AE平分∠BAC,CF平分∠ACD可得∠EAC=∠FCA,即可得到AE∥CF,从而可得四边形AECF是平行四边形;
(2)如图,过点E作EO⊥AC于点O,结合∠B=90°及AE平方∠BAC可得EO=EB,证Rt△ABE≌Rt△AOE可得AO=AB=6,在Rt△ABC中由勾股定理易得AC=10,从而可得OC=4,设CE=x,则EO=BE=BC-CE=8-x,这样在Rt△OEC中由勾股定理建立方程,解方程即可求得CE的值,这样就可求出四边形AECF的面积了.
试题解析:
(1)∵四边形ABCD是矩形,
∴AD∥BC(即AF∥CE),AB∥CD,
∴∠BAC=∠ACD,
又∵AE平分∠BAC,CF平分∠ACD,
∴∠EAC=∠FCA,
∴AE∥CF,
∴四边形AECF是平行四边形;
(2)过点E作EO⊥AC于点O,
∵∠B=90°,AE平分∠BAC,
∴EO=BO,
∵AE=AE,
∴Rt△ABE≌Rt△AOE,
∴AO=AB=6,
∵在Rt△ABC,AC=![]() ,
,
∴OC=AC-AO=4(cm),
设CE=x,则EO=BE=BC-CE=8-x,
∴在Rt△OEC中由勾股定理可得:![]() ,解得:
,解得:![]() ,
,
∴EC=5,
∴S四边形AECF=CE·AB=5×6=30(cm2).


练习册系列答案
相关题目