题目内容
【题目】如图,⊙O是△ABC的外接圆,BC是⊙O的直径,D是劣弧AC中点,BD交AC于点E.
(1)求证:AD2=DEDB;
(2)若BC=13,CD=5,求DE的长.

【答案】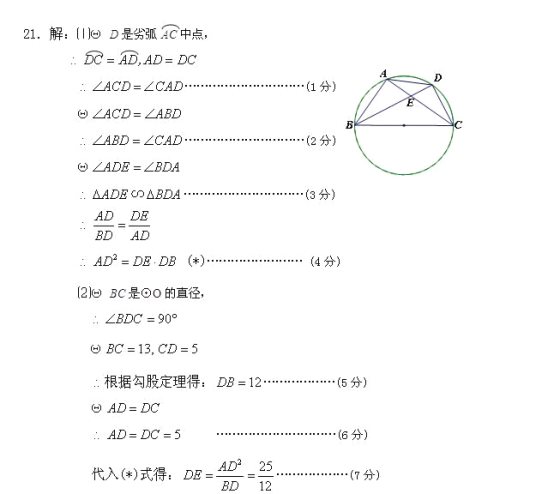
【解析】
(1)由D是劣弧AC的中点,可得∠DAC=∠ABD,即可证明△ABD∽△AED,根据相似三角形的对应边成比例即可得出答案;
(2)由D是劣弧AC中点,可得AD=CD=5,根据CB是直径,可得△BCD是直角三角形,由勾股定理求出BD的长,代入(1)中的AD2=DEDB即可求出DE的长.
(1)证明:∵D是劣弧AC的中点,
∴AD=DC,
∴∠ABD=∠DAC,
又∵∠ADB=∠EDA,
∴△ABD∽△EAD,
∴AD:DE=DB:AD,
∴AD2=DEDB;
(2)∵D是劣弧AC的中点,
∴AD=DC=5,
∵CB是直径,
∴△BCD是直角三角形,
∴BD=![]() ;
;
∵AD2=DEDB,
∴52=12×DE,
解得DE=![]() .
.

练习册系列答案
相关题目