题目内容
如图,在△ABC中,AC=AB=2,∠A=90°,将一块与△ABC全等的三角板的直角顶点放在点C上,一直角边与BC重叠.(1)操作1:固定△ABC,将三角板沿C→B方向平移,使其直角顶点落在BC的中点M,如图2所示,探究:三角板沿C→B方向平移的距离为
(2)操作2:在(1)的情况下,将三角板BC的中点M顺时针方向旋转角度a(0°<a<90°),如图3所示,探究:设三角形板两直角边分别与AB、AC交于点P、Q,观察四边形MPAQ形状的变化,问:四边形MPAQ的面积S是否改变,若不变,求其面积;若改变,试说明理由;
(3)在(2)的情形下,连PQ,设BP=x,记△MPQ的面积为y,试求y关于x的函数关系式,并求x为何值时,y的值是四边形MPAQ的面积的一半,此时,指出四边形MPAQ的形状.
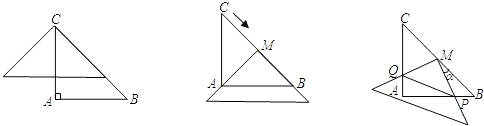
分析:(1)M是BC的中点,三角板沿C→B方向平移的距离为CM,根据勾股定理可求BC,那么CM可求;
(2)连AM,分别证明△MAQ≌△MBP和△MAP≌△MCQ,那么四边形MPAQ的面积S就是△ABC面积的一半;
(3)用四边形MPAQ的面积减去△APQ可得△MPQ的面积,而AQ=PB=x,AP=2-x,据此列出y关于x的函数关系式,将函数值代入函数关系式可得自变量,根据自变量可以判断四边形MPAQ的形状.
(2)连AM,分别证明△MAQ≌△MBP和△MAP≌△MCQ,那么四边形MPAQ的面积S就是△ABC面积的一半;
(3)用四边形MPAQ的面积减去△APQ可得△MPQ的面积,而AQ=PB=x,AP=2-x,据此列出y关于x的函数关系式,将函数值代入函数关系式可得自变量,根据自变量可以判断四边形MPAQ的形状.
解答:解:(1)BC=
=2
∴CM=
BC=
故三角板沿C→B方向平移的距离为:
.
(2)四边形MPAQ的面积S不变,如图,连AM,M是等腰直角三角形ABC斜边BC的中点,
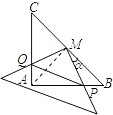
∴AM=BM,而∠QMA=∠PMB=a,∠QAM=∠PBM=45°
∴△MAQ≌△MBP,
同理可得:△MAP≌△MCQ,
∴S四边形MPAQ=S△MAQ+S△MAP=
S△ABC=
×
×2×2=1
(3)y=1-
x(2-x)=
x2-x+1
如果y的值是四边形MPAQ的面积的一半,
则有,
x2-x+1=1×
解得,x=1.
四边形MPAQ为正方形.
| 22+22 |
| 2 |
∴CM=
| 1 |
| 2 |
| 2 |
故三角板沿C→B方向平移的距离为:
| 2 |
(2)四边形MPAQ的面积S不变,如图,连AM,M是等腰直角三角形ABC斜边BC的中点,

∴AM=BM,而∠QMA=∠PMB=a,∠QAM=∠PBM=45°
∴△MAQ≌△MBP,
同理可得:△MAP≌△MCQ,
∴S四边形MPAQ=S△MAQ+S△MAP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)y=1-
| 1 |
| 2 |
| 1 |
| 2 |
如果y的值是四边形MPAQ的面积的一半,
则有,
| 1 |
| 2 |
| 1 |
| 2 |
四边形MPAQ为正方形.
点评:本题考查了旋转的性质、全等三角形的判定、等腰直角三角形的性质、正方形的判定及函数关系式的运用.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B=
20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B= 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为 2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( )
2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( ) 如图,在△ABC中,AB=AC,且∠A=100°,∠B=
如图,在△ABC中,AB=AC,且∠A=100°,∠B=