题目内容
【题目】如图1,将半径为2的圆形纸片沿圆的两条互相垂直的直径AC,BD两次折叠后,得到如图2所示的扇形OAB,然后再沿OB的中垂线EF将扇形OAB剪成左右两部分,则∠OEF=°;右边部分经过两次展开并压平后所得的图形的周长为 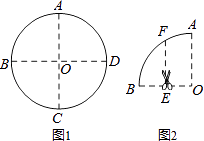
【答案】90;![]() +4
+4 ![]()
【解析】解:如图3, 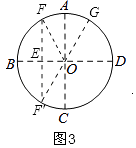
∵EF是OB的中垂线,
∴∠OEF=90°,OE= ![]() OB=
OB= ![]() OF,
OF,
∴∠EFO=30°,∠EOF=60°,
由勾股定理得:EF= ![]() =
= ![]() ,
,
由折叠得:∠F′OF=120°,
∴∠FOA=30°,
∴∠FOG=60°,
则右边部分经过两次展开并压平后所得的图形的周长为:
2 ![]() +2F′F=
+2F′F= ![]() ×2+2×2
×2+2×2 ![]() =
= ![]() +4
+4 ![]() .
.
故答案为:90, ![]() +4
+4 ![]() .
.
根据沿OB的中垂线EF将扇形OAB剪成左右两部分,可知∠OEF=90°,所以E是OB的中点,则OE= ![]() OB=
OB= ![]() OF,则∠EFO=30°,得出
OF,则∠EFO=30°,得出 ![]() 所对的圆周角∠FOG=60°,根据勾股定理求出直角边FE=
所对的圆周角∠FOG=60°,根据勾股定理求出直角边FE= ![]() ,所以FF′=2
,所以FF′=2 ![]() ,从而得出结论.
,从而得出结论.

练习册系列答案
相关题目
【题目】某学校计划开设A,B,C,D四门校本课程供学生选修,规定每个学生必须并且只能选修其中一门,为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将调查结果绘制成如下所示的两个不完整统计图表.
校本课程选修意向统计表
选修课程 | 所占百分比 |
A | a% |
B | 25% |
C | b% |
D | 20% |
请根据图表信息,解答下列问题: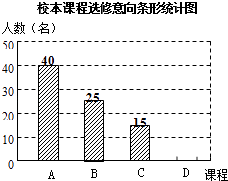
(1)参与调查的学生有名;
(2)在统计表中,a= , b=;
(3)请你补全条形统计图;
(4)若该校共有2000名学生,请你估算该校有多少名学生选修A课程?