题目内容
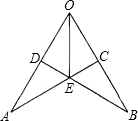
如图,在Rt△ABC中,∠A=90°,AC=6cm,AB=8cm,把AB边翻折,使AB边落在BC边上,点A落在点E处,折痕为BD,则sin∠DBE的值为( )

A.
| B.
| C.
| D.
|

根据折叠的含义可以知道:△ABD≌△EBD,则AD=DE=x,
在直角△ABC中利用勾股定理解得:BC=10,S△ABC=SABD+S△BCD,
即:
AB•AD+
BC•DE=
AB•AC则8x+10x=48,
解得:x=
.
在直角△ABD中,BD=
=
=
,
因而:sin∠DBE=sin∠ABD=
=
.
故选D.
在直角△ABC中利用勾股定理解得:BC=10,S△ABC=SABD+S△BCD,
即:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:x=
| 8 |
| 3 |
在直角△ABD中,BD=
| AB2+AD2 |
82+(
|
8
| ||
| 3 |
因而:sin∠DBE=sin∠ABD=
| AD |
| BD |
| ||
| 10 |
故选D.

练习册系列答案
相关题目