题目内容
【题目】图a是一个长为2m、宽为2n的长方形,沿图中实线用剪刀均分成四块小长方形然后按图b的形状拼成一个大正方形. 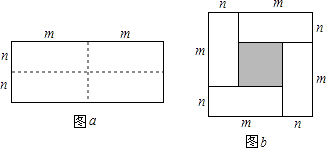
(1)图b中的小正方形的边长等于;
(2)图a中四个长方形的面积和为;图b中四个小长方形的面积和还可以表示为 .
(3)由(2)写出代数式:(m+n)2 , (m﹣n)2 , mn之间的等量关系:;
(4)根据(3)中的等量关系,解决如下问题:若x+y=8,xy=7,则(2x﹣2y)2= .
【答案】
(1)m﹣n
(2)4;mn
(3)(m+n)2﹣4mn
(4)144
【解析】解:(1)图b中的阴影部分的正方形的边长等于长为m,宽为n的长方形的长宽之差,即m﹣n;(2)图a中四个长方形的面积和为4mn;图b中四个小长方形的面积和还可以表示为(m+n)2﹣(m﹣n)2;(3)(m+n)2﹣(m﹣n)2=4mn;(4)(2x﹣2y)2=4(x﹣y)2=4(x+y)2﹣16xy, 当x+y=8,xy=7时,原式=256﹣112=144.

练习册系列答案
相关题目