Question

【题目】在平面直角坐标系中，O为原点，A为x轴正半轴上的动点，经过点A（t，0）作垂直于x轴的直线l，在直线l上取点B，点B在第一象限，AB=4，直线OB：y1=kx（k为常数）．

（1）当t=2时，求k的值；

（2）经过O，A两点作抛物线y2=ax（x﹣t）（a为常数，a＞0），直线OB与抛物线的另一个交点为C．

①用含a，t的式子表示点C的横坐标；

②当t≤x≤t+4时，|y1﹣y2|的值随x的增大而减小；当x≥t+4时，|y1﹣y2|的值随x的增大而增大，求a与t的关系式并直接写出t的取值范围．

Answer 1

【答案】（1）k=2；（2）当t≤x≤t+4时，|y1﹣y2|的值随x的增大而减小；当x≥t+4时，|y1﹣y2|的值随x的增大而增大时，a与t的关系式a=（t≥4）．

【解析】分析：（1）找出当t=2时，B点的坐标，将其代入直线OB:y1=kx中即可；
（2）①用t表示出直线OB的关系式，令y1=y2,即可用含a，t的式子表示点C的横坐标；
②找出的关系式，发现为一个开口向下的抛物线，结合给定条件能够得知，抛物线的对称轴不超过，且抛物线与x轴的另一个交点为(t+4,0).由此可得出a与t的关系式并能知道t的取值范围．

详解：(1)当t=2时,点A的坐标为(2,0)，

∵经过点A(t,0)作垂直于x轴的直线l，在直线l上取点B，点B在第一象限，AB=4，

∴点B的坐标为(2,4).

∵点B在直线OB:y1=kx(k为常数)上，

∴有4=2k，解得：k=2.

(2)①点B(t,4)在直线OB:y1=kx上，

∴有4=kt,解得：

∴

令y1=y2,即

解得：x=0或者

故点C的横坐标

②

∵a>0，

∴a<0，函数图象开口向下，函数图象大体如下图：

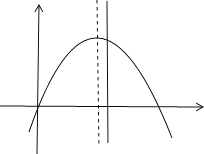
∵当时,的值随x的增大而减小;当时, 的值随x的增大而增大，

∴二次函数的对称轴在x=t的左侧或者重合,而且二次函数与x轴的另一个交点为(t+4,0).

∵

∴有

解得：

二次函数对称轴 即

∵at=1，

∴

故当时,的值随x的增大而减小;当时, 的值随x的增大而增大时,a与t的关系式().