Question

【题目】已知二次函数y=ax2﹣4ax+1

（1）写出二次函数图象的对称轴：_____；

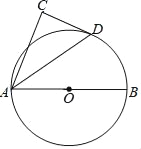
（2）如图，设该函数图象交x轴于点A、B（B在A的右侧），交y轴于点C．直线y=kx+b经过点B、C．

①如果k=﹣，求a的值

②设点P在抛物线对称轴上，PC+PB的最小值为，求点P的坐标．

Answer 1

【答案】（1）直线x=2；（2）① a=3；②.

【解析】分析：

（1）由二次函数的对称轴为直线进行解答即可；

（2）①在由x=0可得y=1，由此可得点C的坐标，从而可得b的值，结合k=可得直线BC的解析式为，由此即可解得点B的坐标，将所得点B的坐标代入中即可解得此时a的值；②由图可知，当点P为BC与抛物线对称轴的交点时，PB+PC最小，此时BC=，结合OC=1，由勾股定理即可解得此时OB的长，从而可得此时点B的坐标，将点B的坐标代入中即可求得此时BC的解析式，由此即可求得此时点P的坐标了.

详解：

（1）二次函数y=ax2﹣4ax+1的图象的对称轴为直线．

故答案为：直线x=2．

（2）①当x=0时，y=1，

∴点C的坐标为（0，1）．

将（0，1）代入y=kx+b，得：b=1．

∵k=，

∴，

当y=0时，有，

解得：x=3，

∴点B的坐标为（3，0）．

将B（3，0）代入y=ax2﹣4ax+1，得：

9a﹣12a+1=0，

解得：a=3；

②当PC+PB取最小值时，点P是直线BC与直线x=2的交点，且PC+PB的最小值=BC=．

∵OC=1，

∴在Rt△OBC中，OB=，

∴此时点B的坐标为，

将点B的坐标代入得：，

解得：，

∴此时直线BC的解析式为：，

∵当时，，

∴点P的坐标为.