Question

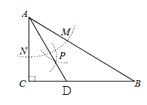
【题目】如图，在△ABC中，∠C＝90°，以A为圆心，任意长为半径画弧分别交AB，AC于点M和N，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于点P，连接AP并延长交BC于点D，则下列结论：①AD是∠BAC的平分线；②若∠B＝30°，则DA＝DB；③AB：AC＝2:1；④点D在AB的垂直平分线上．一定成立的个数为（ ）

A.1个B.2个C.3个D.4个

Answer 1

【答案】B

【解析】

依据角平分线的的作法、等腰三角形的判定、直角三角形中，30°的角所对的直角边等于斜边的一半、垂直平分线的判定，即可得出结论．

①由作图可得，AD是∠BAC的平分线；故①正确；
②当∠B=30°时，∠BAC=60°，
∴∠BAD=∠BAC=30°，
∴∠B=∠BAD，
∴AD=BD，故②正确；
③在直角三角形ABC中，当∠B=30°时，AB：AC＝2:1；

因为不知道∠B的度数，故③错误；
④∵∠B与∠BAD不一定相等，
∴AD与BD不一定相等，
∴点D不一定在AB的垂直平分线上，故④错误；
故选：B．