题目内容
如图,点P在x轴上,以P为圆心的圆与x轴交于点A、B,与y轴交于点C、D,⊙P的半径是2厘米,CD=2厘米.

(1)求点P、点C的坐标;
(2)过点C作⊙P的切线交x轴于点E,连结CP并延长CP交⊙P于点M,连结MD并延长MD交直线CE于点H.若△CDH的外接圆的面积与⊙P的面积的比值是h,求同时满足下列三个条件的抛物线的解析式;
①过点P、E;
②顶点到x轴的距离是h厘米;
③对称轴平行于y轴.
答案:
解析:
解析:
|
(1)∵PO⊥OD,CD=2 ∴C点的坐标为(0, ∵PC=2,OC= ∴P点的坐标为(-1,0). (2)∵CM是⊙P的直径,∴∠CDM= ∵OE∥DH,OC=OD,又∠CEO=∠PCO= ∵⊙P的面积是4π,∴它们的比值h是3. 又所求抛物线过点P(-1,0),E(3,0),可设抛物线的解析式是y=a(x+1)(x-3),即y=a(x-1)2-4a. 由题意知|-4a|=h=3,∴a=± |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
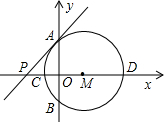 x1,0)、D(x2,0)两点,(x1<x2),x1、x2是方程x(2x+1)=(x+2)2的两根.
x1,0)、D(x2,0)两点,(x1<x2),x1、x2是方程x(2x+1)=(x+2)2的两根. 如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于C,过点C的直线y=2x+b交x轴于D,且⊙P的半径为
如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于C,过点C的直线y=2x+b交x轴于D,且⊙P的半径为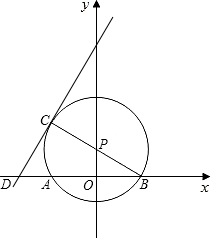 的直线y=2x+b交x轴于D,且⊙P的半径为
的直线y=2x+b交x轴于D,且⊙P的半径为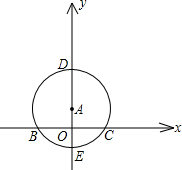 -1)
-1) 交于点D,顺次连接I、D、B三点可以组成等边三角形.过A、B两点的抛物线y=ax2+bx+c的顶点P也在半圆I上.
交于点D,顺次连接I、D、B三点可以组成等边三角形.过A、B两点的抛物线y=ax2+bx+c的顶点P也在半圆I上.