题目内容
如图，点P在y轴上，⊙P交x轴于A，B两点，连接BP并延长交⊙P于C，过点C的直线y=2x+b交x轴于D，且⊙P的半径为| 5 |
| k |
| x |
| A、±4 | ||
| B、-4 | ||
C、-2
| ||
| D、4 |
分析：本题的关键是求出C点的坐标，由于BC是圆P的直径，那么连接AC后三角形ACB就是直角三角形，已知了BC，AB的长，可通过勾股定理求出AC的值，那么即可得出C点的坐标，将C的坐标代入反比例函数的解析式中即可求出k的值．
解答：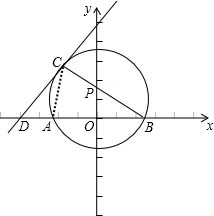
解：连接AC，则AC⊥AB，如图所示：
在直角三角形ABC中，AB=4，BC=2
，
∴AC=2，
∵OP⊥AB，AC⊥AB，
∴AC∥OP，
∵BP=PC，AB=4，
∴OA=OB=2，
∴C的坐标为（-2，2），将C的坐标代入y=
（k＜0）中，可得
k=xy=（-2）×2=-4．
故选B．
解：连接AC，则AC⊥AB，如图所示：在直角三角形ABC中，AB=4，BC=2
| 5 |
∴AC=2，
∵OP⊥AB，AC⊥AB，
∴AC∥OP，
∵BP=PC，AB=4，
∴OA=OB=2，
∴C的坐标为（-2，2），将C的坐标代入y=
| k |
| x |
k=xy=（-2）×2=-4．
故选B．
点评：本题主要考查了用待定系数法求反比例函数的方法，难度适中，主要掌握用数形结合的思想求出C点的坐标是解题的关键．
练习册系列答案
相关题目
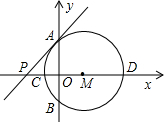x1，0）、D（x2，0）两点，（x1＜x2），x1、x2是方程x（2x+1）=（x+2）2的两根．
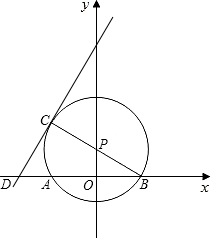的直线y=2x+b交x轴于D，且⊙P的半径为
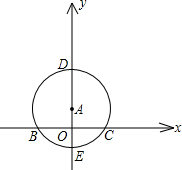-1）
交于点D，顺次连接I、D、B三点可以组成等边三角形．过A、B两点的抛物线y=ax2+bx+c的顶点P也在半圆I上．