题目内容
在△ABC中，∠A=47°，高BE、CF所在直线交于点O，且点E、F不与点B、C重合，则∠BOC=______．
本题要分两种情况讨论如图：
（1）当交点在三角形内部时，在四边形AFOE中，∠AFC=∠AEB=90°，∠A=47°，
根据四边形内角和等于360°得，
∠EOF=180°-∠A=180°-47°=133°．
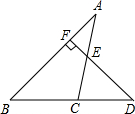
（2）当交点在三角形外部时，在△AFC中，∠A=47°，∠AFC=90°，
故∠1=180°-90°-47°=43°，
∵∠1=∠2，
∴在△CEO中，∠2=43°，∠CEO=90°，
故∠EOF=180°-90°-43°=47度．
答：∠BOC=47或133度．
（1）当交点在三角形内部时，在四边形AFOE中，∠AFC=∠AEB=90°，∠A=47°，
根据四边形内角和等于360°得，
∠EOF=180°-∠A=180°-47°=133°．
（2）当交点在三角形外部时，在△AFC中，∠A=47°，∠AFC=90°，
故∠1=180°-90°-47°=43°，
∵∠1=∠2，
∴在△CEO中，∠2=43°，∠CEO=90°，
故∠EOF=180°-90°-43°=47度．
答：∠BOC=47或133度．
练习册系列答案
53随堂测系列答案
相关题目
