Question

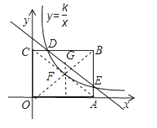
【题目】如图，已知矩形OABC的两边OA，OC分别在x轴，y轴的正半轴上，且点B（4，3），反比例函数y=图象与BC交于点D，与AB交于点E，其中D（1，3）．
（1）求反比例函数的解析式及E点的坐标；
（2）求直线DE的解析式；
（3）若矩形OABC对角线的交点为F (2,)，作FG⊥x轴交直线DE于点G．
①请判断点F是否在此反比例函数y=的图象上，并说明理由；
②求FG的长度．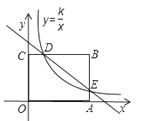

Answer 1

【答案】解：（1）∵D （1，3）在反比例函数y= 的图象上，
∴3=，
解得k=3
∴反比例函数的解析式为：y=，
∵B（4，3），
∴当x=4时，y=，
∴E（4，）；
（2）设直线DE的解析式为y=kx+b（k≠0），
∵D（1，3），E（4，），
∴，
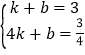解得，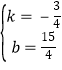
∴直线DE的解析式为：y=﹣x+；
（3）①点F在反比例函数的图象上．
理由如下：
∵当x=2时，y==
∴点F在反比例函数 y=的图象上．
②∵x=2时，y=﹣x+=，
∴G点坐标为（2，）
∴FG=﹣=．

【解析】（1）把点D（1，3）直接代入反比例函数的解析式即可得出k的值，进而得出反比例函数的解析式，再根据B（4，3）可知，直线AB的解析式x=4，再把x=4代入反比例函数关系式即可求出E点坐标；
（2）根据D、E两点的坐标用待定系数法求出直线DE的解析式；
（3）①直接把点F的坐标代入（1）中所求的反比例函数解析式进行检验即可；
②求出G点坐标，再求出FG的长度即可．