题目内容
 用配方法将二次函数y=x2-2x-3化为y=a(x-h)2+k的形式(其中h,k为常数),写出这个二次函数图象的顶点坐标和对称轴方程,并在直角坐标系中画出他的示意图.
用配方法将二次函数y=x2-2x-3化为y=a(x-h)2+k的形式(其中h,k为常数),写出这个二次函数图象的顶点坐标和对称轴方程,并在直角坐标系中画出他的示意图.分析:先用配方法把二次函数y=x2-2x-3化为顶点式的形式,再根据其顶点式直接写出函数的对称轴方程及顶点坐标,求出抛物线与x轴的交点坐标,利用描点法画出函数图象即可.
解答: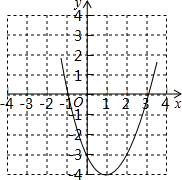 解:∵y=x2-2x-3=(x-1)2-4,
解:∵y=x2-2x-3=(x-1)2-4,
∴顶点坐标为(1,-4),对称轴方程为 x=1.
∵函数二次函数y=x2-2x-3的顶点坐标为(1,-4),与x轴的交点为(3,0),(-1,0),
∴其图象为:
 解:∵y=x2-2x-3=(x-1)2-4,
解:∵y=x2-2x-3=(x-1)2-4,∴顶点坐标为(1,-4),对称轴方程为 x=1.
∵函数二次函数y=x2-2x-3的顶点坐标为(1,-4),与x轴的交点为(3,0),(-1,0),
∴其图象为:
点评:本题考查的是二次函数的性质、二次函数的顶点式及用描点法画二次函数的图象,能利用配方法把二次函数的一般形式化为顶点式是解答此题的关键.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
用配方法将二次函数y=3x2-4x-2写成形如y=a(x+m)2+n的形式,则m、n的值分别是( )
A、m=
| ||||
B、m=-
| ||||
| C、m=2,n=6 | ||||
| D、m=2,n=-2 |