题目内容
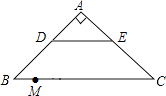
【题目】如图,![]() 且
且![]() 点在线段
点在线段![]() 上,连接
上,连接![]() .
.
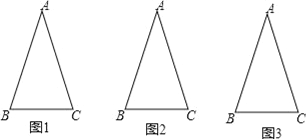
(1)如图1,若![]() 求线段
求线段![]() 的长;
的长;

(2)如图1,若![]() 求证:
求证:![]()
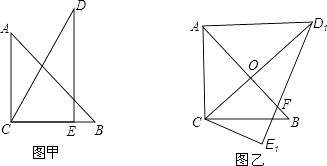
(3)如图2,在第(2)问的条件下,若点![]() 在
在![]() 的延长线上时,连接
的延长线上时,连接![]() 的面积为
的面积为![]() 的面积为
的面积为![]() 的面积为
的面积为![]() .直接写出
.直接写出![]() 之间的数量关系.
之间的数量关系.

【答案】(1)线段AB的长为6;(2)见解析;(3)c+a=2b.
【解析】
(1)通过“SAS”可证△ACD≌△BCE,由此可得BE=AD=4,结合AE=2即可得解;
(2)在AD上取一点H,使得AH=AE,先证△ACH≌△ACE,可得CH=CE,进而可证CH=CD,利用三线合一可得DH=2DF,最后根据AD=DH+AH等量代换即可得证;
(3)过点C作CG⊥AB于点G,同理可证△ACD≌△BCE,进而得BE=AD,∠CAD=∠B=45°,∠D=∠CEB,证得CF∥AB便可证得S△AEC=S△AEF=a,再证△CFD≌△CGE可得S△CGE=S△CFD=b,
根据三线合一可得AG=BG便可得S△BCG=S△BCG,进而得解.
(1)证明:∵∠ACB=∠DCE=90°,
∴∠ACE+∠ECB=∠ACE+∠DCA,
∴∠ECB=∠DCA,
在△ACD与△BCE中,

∴△ACD≌△BCE(SAS),
∴BE=AD,
∵AD=4,
∴BE=4,
又∵AE=2,
∴AB=AE+BE=6,
∴线段AB的长为6;
(2)证明:如图,在AD上取一点H,使得AH=AE,连接CH,

∵AC=BC,∠ACB=90°,
∴∠B=∠CAB=45°,
∵△ACD≌△BCE,
∴∠CAD=∠B=45°,BE=AD,
在△ACH与△ACE中,

∴△ACH≌△ACE(SAS),
∴CH=CE,
∵CD=CE,
∴CH=CD,
又∵CF⊥AD,
∴DF=FH,
∴DH=2DF,
∵AD=DH+AH,
∴BE=2DF+AE;
(3)解:如图,过点C作CG⊥AB于点G,

∵∠ACB=∠DCE=90°,
∴∠ACE+∠ACB=∠ACE+∠DCE,
∴∠ECB=∠DCA,
在△ACD与△BCE中,

∴△ACD≌△BCE(SAS),
∴BE=AD,∠CAD=∠B=45°,∠D=∠CEB,
∴∠BAD=∠CAD+∠CAB=90°,
又∵CF⊥AD,
∴CF∥AB,
∴S△AEC=S△AEF=a,
∵△ACD≌△BCE,
∴S△ACD=S△BCE,
∴CF⊥AD,CG⊥AB,
∴∠CFD=∠CGE=90°,
在△CFD与△CGE中,
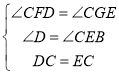
∴△CFD≌△CGE(AAS),
∴S△CGE=S△CFD=b,
∴S△CGA=S△CGE-S△AEC=b-a,
∵S△BCE=c,
∴S△BCG=S△BCE-S△CGE=c-b,
∵AC=BC,CG⊥AB,
∴AG=BG,
∴S△BCG=S△BCG,
∴c-b=b-a,
即:c+a=2b.