题目内容
已知D、E、F分别为等腰△ABC边BC、CA、AB上的点,如果
 ,
, ,∠FDE=∠B,那么AF的长为( )
,∠FDE=∠B,那么AF的长为( )
A. B.
B.  C.
C.  D.
D. 
C.
解析试题分析:由AE和CE的长可求出AC的长,因为△ABC是等腰三角形,所以AB=AC,若要求AF 的长,可求出BF的长即可.而通过证明△DBF∽△DCE即可求出BF的长,问题得解.
解:∵AB=AC,
∴∠B=∠C,
∵∠BFD=180°-∠B-∠FDB,∠EDC=180°-∠FDE-∠FDB,
又∵∠FDE=∠B,
∴∠BFD=∠EDC,
∴△DBF∽△DCE,
∴BD:CE=BF:CD,
∵BD=2,CD=3,CE=4,
∴2:4=BF:3,
∴BF=1.5,
∵AC=AE+CE= +4=5.5,
+4=5.5,
∴AB=5.5,
∴AF=AB-BF=5.5-1.5=4,
故选C.
考点:1.相似三角形的判定与性质;2.等腰三角形的性质.

练习册系列答案
相关题目
对一个图形进行放缩时,下列说法中正确的是( )
| A.图形中线段的长度与角的大小都会改变; |
| B.图形中线段的长度与角的大小都保持不变; |
| C.图形中线段的长度保持不变、角的大小可以改变; |
| D.图形中线段的长度可以改变、角的大小保持不变. |
如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3米,CA=1米,则树的高度为( )
| A.3米 | B.4米 | C.4.5米 | D.6米 |
如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行. 张强扛着箱子(人与箱子的总高度约为2.2m)乘电梯刚好安全通过,请你根据图中数据回答,两层楼之间的高约为( )
| A.5.5m | B.6.2m | C.11 m | D.2.2 m |

 DE // AC,EF // AB ( )
DE // AC,EF // AB ( )
 ,
,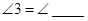 ( )
( ) ( )
( ) ( )
( ) ( )
( )
 .
.

