题目内容
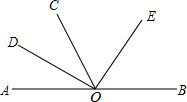 如图,已知∠AOC与∠BOC是邻补角,OD是∠AOC的角平分线,OE是∠BOC的平分线.
如图,已知∠AOC与∠BOC是邻补角,OD是∠AOC的角平分线,OE是∠BOC的平分线.(1)求∠DOE的度数;
(2)指出∠BOE的余角.
分析:(1)根据OD是∠AOC的角平分线,OE是∠BOC的平分线可得∠DOC=
∠AOC,∠COE=
∠BOC,又根据∠DOE=∠DOC+∠COE,可求得∠DOE=
∠AOB=90°;
(2)∠BOE的余角为∠DOC和∠AOC.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)∠BOE的余角为∠DOC和∠AOC.
解答:解:(1)∵OD是∠AOC的角平分线,OE是∠BOC的平分线,
∴∠DOC=
AOC,∠COE=
∠BOC,
∵∠DOE=∠DOC+∠COE,
∴∠DOE=
∠AOC+
∠BOC=
∠AOB=90°;
(2)由(1)得,DO⊥EO,
∵∠BOE=∠COE,∠AOD=∠COD,
∴∠BOE的余角为∠DOC和∠AOC.
∴∠DOC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠DOE=∠DOC+∠COE,
∴∠DOE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)得,DO⊥EO,
∵∠BOE=∠COE,∠AOD=∠COD,
∴∠BOE的余角为∠DOC和∠AOC.
点评:本题考查了余角和补角以及角平分线的定义,解答本题的关键是掌握互余两角和为90°.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
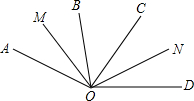 如图,已知∠AOC与∠BOD有公共顶点O,OM平分∠AOB,ON平分∠COD,若∠MON=α,∠BOC=β,试用α,β表示∠AOD.
如图,已知∠AOC与∠BOD有公共顶点O,OM平分∠AOB,ON平分∠COD,若∠MON=α,∠BOC=β,试用α,β表示∠AOD.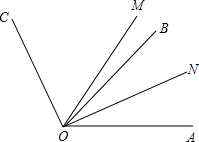 如图,已知∠AOC与∠AOB互为补角,OM、ON分别是∠AOC、∠AOB的平分线,且∠MON=35°,求∠COB的补角和∠AON的余角.
如图,已知∠AOC与∠AOB互为补角,OM、ON分别是∠AOC、∠AOB的平分线,且∠MON=35°,求∠COB的补角和∠AON的余角.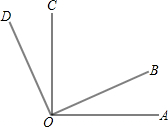 如图,已知∠AOC与∠BOD都是直角,∠BOC=65°
如图,已知∠AOC与∠BOD都是直角,∠BOC=65°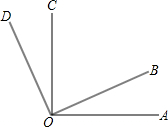 如图,已知∠AOC与∠BOD都是直角,∠BOC=65°
如图,已知∠AOC与∠BOD都是直角,∠BOC=65°