题目内容
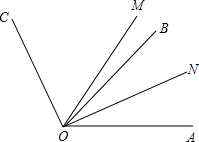 如图,已知∠AOC与∠AOB互为补角,OM、ON分别是∠AOC、∠AOB的平分线,且∠MON=35°,求∠COB的补角和∠AON的余角.
如图,已知∠AOC与∠AOB互为补角,OM、ON分别是∠AOC、∠AOB的平分线,且∠MON=35°,求∠COB的补角和∠AON的余角.分析:根据角平分线的定义可得∠AOM=
∠AOC,∠AON=
∠AOB,再结合图形表示出∠MON并求出∠AOC-∠AOB的度数,又∠AOC与∠AOB互为补角,两式联立解方程组求出∠AOC与∠AOB的度数,然后求出∠COB,再根据互为补角的和等于180°列式求解得到∠COB的补角;根据角平分线的定义求出∠AON的度数,再根据互为余角的和等于90°列式求解得到∠AON的余角.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵OM、ON分别是∠AOC、∠AOB的平分线,
∴∠AOM=
∠AOC,∠AON=
∠AOB,
∴∠MON=∠AOM-∠AON=
∠AOC-
∠AOB=35°,
∴∠AOC-∠AOB=70°,
∵∠AOC与∠AOB互为补角,
∴∠AOC+∠AOB=180°,
联立
,
解得∠AOC=125°,∠AOB=55°,
∴∠COB=∠AOC-∠AOB=125°-55°=70°,
∴∠COB的补角=180°-70°=110°,
∵∠AON=
∠AOB=
×55°=27.5°,
∴∠AON的余角=90°-27.5°=62.5°.
故答案为:110°,62.5°.
∴∠AOM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠AOM-∠AON=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AOC-∠AOB=70°,
∵∠AOC与∠AOB互为补角,
∴∠AOC+∠AOB=180°,
联立
|
解得∠AOC=125°,∠AOB=55°,
∴∠COB=∠AOC-∠AOB=125°-55°=70°,
∴∠COB的补角=180°-70°=110°,
∵∠AON=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AON的余角=90°-27.5°=62.5°.
故答案为:110°,62.5°.
点评:本题考查了互为补角与互为余角的性质,角平分线的定义,准确识图求出用∠AOC-∠AOB表示出∠MON并求出其度数是解题的关键,也是本题的难点.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
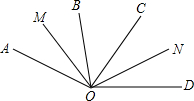 如图,已知∠AOC与∠BOD有公共顶点O,OM平分∠AOB,ON平分∠COD,若∠MON=α,∠BOC=β,试用α,β表示∠AOD.
如图,已知∠AOC与∠BOD有公共顶点O,OM平分∠AOB,ON平分∠COD,若∠MON=α,∠BOC=β,试用α,β表示∠AOD.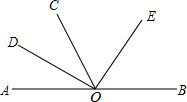 如图,已知∠AOC与∠BOC是邻补角,OD是∠AOC的角平分线,OE是∠BOC的平分线.
如图,已知∠AOC与∠BOC是邻补角,OD是∠AOC的角平分线,OE是∠BOC的平分线.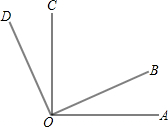 如图,已知∠AOC与∠BOD都是直角,∠BOC=65°
如图,已知∠AOC与∠BOD都是直角,∠BOC=65°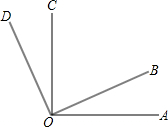 如图,已知∠AOC与∠BOD都是直角,∠BOC=65°
如图,已知∠AOC与∠BOD都是直角,∠BOC=65°