题目内容
【题目】已知抛物线y=ax2+bx+c（a≠0）经过原点，顶点为A（h，k）（h≠0）．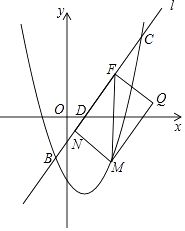
（1）当h=1，k=2时，求抛物线的解析式；
（2）若抛物线y=tx2（t≠0）也经过点A，过a与t之间的关系式；
（3）在（2）的条件下，已知a=﹣ 
，直线l：y= 
x﹣1与抛物线y=tx2﹣ 
x﹣7交于点B，C，与x轴，y轴交于点D，E，点M在抛物线y=tx2﹣ x﹣7上，且点M的横坐标为m（0＜m＜6）．MF∥y轴交于直线l于点F，点N在直线l上，且四边形MNFQ为矩形（如图），若矩形MNFQ的周长为P，求P的最大值．
【答案】
（1）解：∵由题意可知抛物线顶点坐标为（1，2），
∴可设抛物线解析式为y=a（x﹣1）2+2，
∵抛物线过原点，
∴0=a（0﹣1）2+2，解得a=﹣2，
∴抛物线解析式为y=﹣2（x﹣1）2+2；
（2）解：∵抛物线y=tx2（t≠0）也经过点A，
∴k=th2，
∴y=a（x﹣h）2+k=a（x﹣h）2+th2，
∵当x=0时y=0，
∴0=ah2+th2，
∵h≠0，
∴a+t=0，即a=﹣t；
（3）解：由（2）可知a=﹣t，
∴当a=-
时，t= ，
∴M（m， m2-
m-7），F（m，
m﹣1），
∴FM=（m﹣1）﹣（m2﹣m﹣7）=﹣m2+2m+6，
又在y= x﹣1中，
当x=0时，y=﹣1，y=0时，x=
，
∴OD=，OE=1，
∴DE=
=
，
∵MF∥y轴，
∴∠DEO=∠MFN，
在矩形MNFQ中，NF=MF·cos∠MFN=MF·
=
MF，
MN=MF·sin∠MFN=MF·
=
MF，
∴P=2（MN+NF）=
MF=（﹣m2+2m+6）=-
m2+
m+
=﹣（m﹣2）2+ 
，
∵0＜m＜6，﹣＜0，
∴当m=2时，P取最大值，最大值为 ．
【解析】（1）由题可知抛物线顶点坐标为（1，2），依此可设抛物线解析式为y=a（x﹣1）2+2，又抛物线过原点，从而得出抛物线解析式.
（2）将A点坐标代入抛物线y=tx2（t≠0），再将（0，0）代入y=a（x﹣h）2+k，由此即可得出即a=﹣t.
（3）由（2）知a=﹣t，由题意知M（m， m2-m-7），F（m，m﹣1），从而得FM=﹣m2+2m+6；根据已知条件得OD=，OE=1，
根据勾股定理得DE=，由平行线性质得∠DEO=∠MFN；在矩形MNFQ中，由锐角三角函数定义得NF=MF，MN=MF，从而得出P=2（MN+NF）=﹣（m﹣2）2+ ，根据二次函数得性质和自变量的取值范围0＜m＜6得当m=2时，Pmin= ．
【考点精析】关于本题考查的勾股定理的概念和矩形的性质，需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；矩形的四个角都是直角，矩形的对角线相等才能得出正确答案．
