题目内容
已知关于x的方程(m+3)x2+x+m2+2m-3=0的一根为0，另一根不为0，则m的值为（ ）
| A．1 | B．-3 | C．1或-3 | D．以上均不对 |
A
∵关于x的方程（m+3）x2+x+m2+2m-3=0的一根为0，
∴（m+3）×02+0+m2+2m-3=0，
即m2+2m-3=0，
解得：m=1或-3．
又关于x的方程的另一根不为0，
所以△≥0，
即1-4（m+3）（m2+2m-3）≥0，
解得：m∈（-∞，+∞），当m=-3时，m+3=0，此方程不可能有两根，
故选A．
∴（m+3）×02+0+m2+2m-3=0，
即m2+2m-3=0，
解得：m=1或-3．
又关于x的方程的另一根不为0，
所以△≥0，
即1-4（m+3）（m2+2m-3）≥0，
解得：m∈（-∞，+∞），当m=-3时，m+3=0，此方程不可能有两根，
故选A．
练习册系列答案
名校课堂系列答案
相关题目
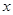，则下列方程正确的是（ ）
的两根，则
的值是（ ）
有两个不相等的实数根．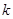
的取值范围； 
有一个相同的根，求此时
的值．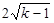
x-1=0有两个不相等的实数根，则k的取值范围是
转化为一元二次方程的一般形式是 。