题目内容
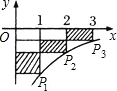 (1)如图在反比例函数y=-
(1)如图在反比例函数y=-| 4 |
| x |
(2)若一次函数y=mx-4的图象与(1)中的反比例函数y=-
| 4 |
| x |
分析:(1)解法一:把横坐标代入函数解析式分别求出三点P1、P2、P3的坐标,然后根据矩形的面积公式分别求出S1、S2、S3,相加即可;解法二:根据长与宽相等的矩形面积相等,可以把后两个矩形的平移到最左边两个空白处,于是,图中阴影部分的面积之和等于如图以点P1为顶点的矩形的面积,再利用反比例函数图象进行解答;
(2)两式联立组成方程组,整理得到关于x的一元二次方程,利用判别式△≥0列式求解即可.
(2)两式联立组成方程组,整理得到关于x的一元二次方程,利用判别式△≥0列式求解即可.
解答: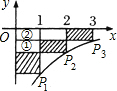 解:(1)解法一:根据题意,当x=1时,y=-4,
解:(1)解法一:根据题意,当x=1时,y=-4,
当x=2时,y=-2,
当x=3时,y=-
,
∴三点P1、P2、P3的坐标分别为P1(1,-4),P2(2,-2),P3(3,-
),
∴S1=1×(|-4|-|-2|)=2,S2=1×(|-2|-|-
|)=
,S3=1×|-
|=
,
∴S1+S2+S3=2+
+
=4;
解法二:如图,根据长与宽相等的矩形的面积相等,后两个阴影部分可以分别平移到①②的位置,
∵当x=1时,y=-4,
∴点P1的坐标为P1(1,-4),
∴S1+S2+S3=1×|-4|=4;
(2)一次函数y=mx-4与反比例函数y=-
(x>0)联立得,
,
整理得mx2-4x+4=0,
∵两函数图象有交点,
∴△=b2-4ac=(-4)2-4×4m=16-16m≥0,
解得m≤1,
∵y=mx-4是一次函数,
∴m≠0,
∴m的取值范围是x≤1且m≠0.
故答案为:(1)4;(2)m≤1且m≠0.
 解:(1)解法一:根据题意,当x=1时,y=-4,
解:(1)解法一:根据题意,当x=1时,y=-4,当x=2时,y=-2,
当x=3时,y=-
| 4 |
| 3 |
∴三点P1、P2、P3的坐标分别为P1(1,-4),P2(2,-2),P3(3,-
| 4 |
| 3 |
∴S1=1×(|-4|-|-2|)=2,S2=1×(|-2|-|-
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
∴S1+S2+S3=2+
| 2 |
| 3 |
| 4 |
| 3 |
解法二:如图,根据长与宽相等的矩形的面积相等,后两个阴影部分可以分别平移到①②的位置,
∵当x=1时,y=-4,
∴点P1的坐标为P1(1,-4),
∴S1+S2+S3=1×|-4|=4;
(2)一次函数y=mx-4与反比例函数y=-
| 4 |
| x |
|
整理得mx2-4x+4=0,
∵两函数图象有交点,
∴△=b2-4ac=(-4)2-4×4m=16-16m≥0,
解得m≤1,
∵y=mx-4是一次函数,
∴m≠0,
∴m的取值范围是x≤1且m≠0.
故答案为:(1)4;(2)m≤1且m≠0.
点评:本题综合考查了反比例函数图象的性质,点的坐标,三角形的面积,以及判别式的利用,综合性较强,求解时要注意用点的坐标表示边长的方法,不要出错.

练习册系列答案
相关题目

 如图,反比例函数
如图,反比例函数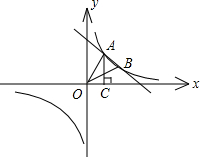 如图,反比例函数
如图,反比例函数 的图象经过A、B两点,点A、B的横坐标分别为2、4,过A作AC⊥x轴,垂足为C,且△AOC的面积等于4.
的图象经过A、B两点,点A、B的横坐标分别为2、4,过A作AC⊥x轴,垂足为C,且△AOC的面积等于4.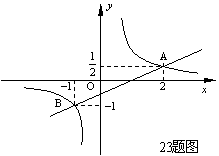
 (x>0)的图像 上运动,那么点B在函数 (填函数解析式)的图像上运动.
(x>0)的图像 上运动,那么点B在函数 (填函数解析式)的图像上运动.