Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ‘ń∂ŃŌ¬√ś≤ńŃŌ≤ĘĹ‚ĺŲ”–Ļōő Ő‚£ļő“√«÷™Ķņ£ļ 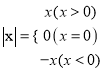 £¨Ō÷‘ŕő“√«Ņ…“‘”√’‚“ĽĹŠ¬ŘņīĽĮľÚļ¨”–ĺÝ∂‘÷ĶĶń Ĺ◊”°£
£¨Ō÷‘ŕő“√«Ņ…“‘”√’‚“ĽĹŠ¬ŘņīĽĮľÚļ¨”–ĺÝ∂‘÷ĶĶń Ĺ◊”°£
»ÁĽĮľÚīķ ż Ĺ|x+1|+|x-2| Ī£¨Ņ…ŃÓx+1=0 ĽÚ x-2=0£¨∑÷Īū«ůĶ√x=-1£¨x=-2(≥∆-1£¨2∑÷Īūő™|x+1|ļÕ|x-2|ĶńŃ„Ķ„÷Ķ°£
‘ŕ”–ņŪ ż∑∂őßńŕ£¨Ń„Ķ„÷Ķx=-1ļÕx=2£¨Ņ…Ĺę»ęŐŚ”–ņŪ ż∑÷≥…≤Ľ÷ōłī«“≤Ľ“Ҭ©Ķń»ÁŌ¬3÷÷«ťŅŲ£ļ£®1£©<-1£Ľ£®2£©-1![]() x
x![]() (3)x
(3)x![]() -2
-2
|ī”∂ÝĽĮľÚ Ĺ◊”|x+1|+|x-2|Ņ…∑÷“‘Ō¬3÷÷«ťŅŲ£ļ
£®1£©ĶĪx<-1 Ī£¨‘≠ Ĺ=-£®x+1£©-£®x-2£©=-2x+1£Ľ
£®2£©ĶĪ-1![]() x
x![]() Ī£¨‘≠ Ĺ= x+1-(x-2) =3£Ľ
Ī£¨‘≠ Ĺ= x+1-(x-2) =3£Ľ
£®3£©ĶĪx![]() -2 Ī£¨‘≠ Ĺ=x+1+(x-2)=2x-1
-2 Ī£¨‘≠ Ĺ=x+1+(x-2)=2x-1
◊Ř…Ōňý Ų£¨‘≠ Ĺ=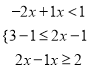
Õ®Ļż“‘…Ō‘ń∂Ń£¨«Žń„Ĺ‚ĺŲ“‘Ō¬ő Ő‚£ļ°į£®1£©ĽĮľÚ|x-4|-|x+2|
(2)|x|+|x+1|+|x+2|
°ĺīūįł°Ņ£®1£©![]() =
=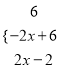
 £Ľ
£Ľ
£®2£©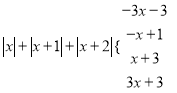
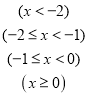 .
.
°ĺĹ‚őŲ°Ņ ‘Ő‚∑÷őŲ£ļłýĺ›ĺÝ∂‘÷ĶĶń–‘÷ £¨Ņ…ĽĮľÚĺÝ∂‘÷Ķ£¨łýĺ›’Ż ĹĶń‘ňň„£¨Ņ…Ķ√īūįł£ģ
‘Ő‚Ĺ‚őŲ£ļ
£®1£©ĶĪ![]() Ī£¨‘≠ Ĺ=
Ī£¨‘≠ Ĺ=![]() £¨
£¨
ĶĪ![]() Ī£¨‘≠ Ĺ=
Ī£¨‘≠ Ĺ=![]() £¨
£¨
ĶĪ ![]() Ī£¨‘≠ Ĺ=
Ī£¨‘≠ Ĺ= ![]() £¨
£¨
◊Ř…Ōňý Ų£¨ ![]() =
=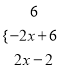
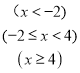
£®2£©ĶĪ![]() Ī£¨‘≠ Ĺ=
Ī£¨‘≠ Ĺ=![]()
ĶĪ![]() Ī£¨‘≠ Ĺ=
Ī£¨‘≠ Ĺ=![]()
ĶĪ![]() Ī£¨‘≠ Ĺ=
Ī£¨‘≠ Ĺ=![]()
ĶĪ![]() Ī£¨‘≠ Ĺ=
Ī£¨‘≠ Ĺ= ![]()
◊Ř…Ōňý Ų£¨ 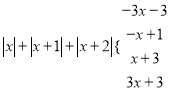
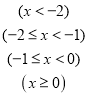 .
.

 ń‹Ń¶∆ņľŘŌĶŃ–īūįł
ń‹Ń¶∆ņľŘŌĶŃ–īūįł Ő∆”°őńĽĮŅő Ī≤‚∆ņŌĶŃ–īūįł
Ő∆”°őńĽĮŅő Ī≤‚∆ņŌĶŃ–īūįł°ĺŐ‚ńŅ°Ņő™‘Ų«ŅĻę√ŮĹŕňģ“‚ ∂£¨ļŌņŪņŻ”√ňģ◊ ‘ī£¨ń≥ –≤…”√°įĹ◊Ő› ’∑—°Ī£¨ĪÍ◊ľ»ÁŌ¬ĪŪ£ļ
”√ňģŃŅ | Ķ•ľŘ |
≤Ľ≥¨Ļż6m3 Ķń≤Ņ∑÷ | 2‘™/ m3 |
≥¨Ļż6m3≤Ľ≥¨Ļż10m3Ķń≤Ņ∑÷ | 4‘™/m3 |
≥¨≥Ų10m3Ķń≤Ņ∑÷ | 8‘™/m3 |
∆©»Á£ļń≥”√Ľß2‘¬∑›”√ňģ9m3£¨‘Ú”¶Ĺ…ňģ∑—£ļ2°Ń6+4°Ń(9£≠6)=24(‘™)
(1)ń≥”√Ľß3‘¬”√ňģ15 m3”¶Ĺ…ňģ∑—∂ŗ…Ŕ‘™£Ņ
(2) “—÷™ń≥”√Ľß4‘¬∑›Ĺ…ňģ∑—20‘™£¨«ůł√”√Ľß4‘¬∑›Ķń”√ňģŃŅ£Ľ
(3) »ÁĻŻł√”√Ľß5°Ę6‘¬∑›Ļ≤”√ňģ20m3 £®6‘¬∑›”√ňģŃŅ≥¨Ļż5‘¬∑›”√ňģŃŅ£©£¨Ļ≤ĹĽňģ∑—64‘™£¨‘Úł√Ľßĺ”√Ů5°Ę6‘¬∑›łų”√ňģ∂ŗ…ŔŃĘ∑Ĺ√◊£Ņ