Question

如图所示，已知△ABC中，∠A=84°，点B、C、M在一条直线上，∠ABC和∠ACM两角的平分线交于点P₁，∠P₁BC和∠P₁CM两角的平分线交于点P₂，∠P₂BC和∠P₂CM两角的平分线交于点P₃，则∠P₃的度数是________．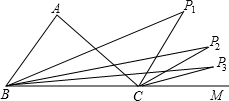

Answer 1

10.5°
分析：根据三角形的外角的性质，得∠P₁=∠P₁CM-∠P₁BC，根据角平分线的定义和三角形的外角的性质，得∠P₁CM-∠P₁BC=（∠ACM-∠ABC）=∠A；同理，得∠P₁=∠P₂，∠P₃=∠P₂．
解答：∵∠ABC和∠ACM两角的平分线交于点P₁，
∴∠P₁=∠P₁CM-∠P₁BC=（∠ACM-∠ABC）=∠A=42°．
同理，得∠P₁=∠P₂=21°，∠P₃=∠P₂=10.5°．
点评：此题综合运用了三角形的外角的性质、三角形的内角和定理以及角平分线定义．
注意结论：三角形的一个内角的角平分线和不相邻的一个外角的平分线相交所成的锐角等于第三个内角的一半．