题目内容
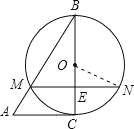
【题目】如图,在△ABC中,以BC为直径的⊙O交AB于M,弦MN∥AC且MN交BC于点E,ME=1,BM=2,BE=![]() .
.

(1)求证AC是⊙O的切线;
(2)求弧NC的长度.
【答案】(1)证明见解析(2)![]()
【解析】
试题分析:(1)根据勾股定理的逆定理证明∠BEM=90°,根据平行线的性质得到∠ACB=90°,根据切线的判定定理证明;
(2)根据正弦的定义和垂径定理求出∠CON=60°,利用弧长公式计算即可.
试题解析:(1)∵ME=1,BM=2,BE=![]() ,
,
∴ME2+BE2=1+3=4,BM2=4,
∴ME2+BE2=BM2,
∴∠BEM=90°,又MN∥AC,
∴∠ACB=∠BEM=90°,
∴AC是⊙O的切线;
(2)连接ON,
∵∠BEM=90°,ME=1,BM=2,
∴∠B=30°,![]() ,NE=ME=1,
,NE=ME=1,
∴∠CON=60°,
ON=![]() ,
,
故弧NC的长度为: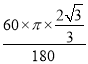 =
=![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目